题目内容
如图,平面四边形 的4个顶点都在球
的4个顶点都在球 的表面上,
的表面上, 为球
为球 的直径,
的直径, 为球面上一点,且
为球面上一点,且 平面
平面  ,
, ,点
,点 为
为 的中点.
的中点.
(1) 证明:平面 平面
平面 ;
;
(2) 求点 到平面
到平面 的距离.
的距离.
(1)详见解析;(2)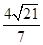
解析试题分析:本小题通过立体几何的相关知识,具体涉及到直线与直线垂直的判断、线面的平行关系的判断以及二面角的求法等有关知识,考查考生的空间想象能力、推理论证能力,对学生的数形结合思想的考查也有涉及,本题是一道立体几何部分的综合题,属于中档难度试题.(1)借助几何体的性质,得到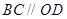 ,借助线面平行的判定定理得到线面平行,进而利用面面平行的判定定理证明平面
,借助线面平行的判定定理得到线面平行,进而利用面面平行的判定定理证明平面 平面
平面 ;(2)利用等体积求解几何体的高,即为点
;(2)利用等体积求解几何体的高,即为点 到平面
到平面 的距离.
的距离.
试题解析:(1) 证明: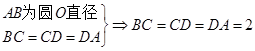 且
且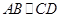 ,
,
则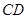 平行且等于
平行且等于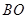 ,即四边形
,即四边形 为平行四边形,所以
为平行四边形,所以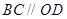 .
.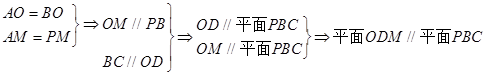 (6分)
(6分)
(2) 由图可知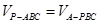 ,即
,即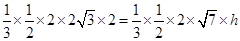
则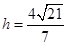 ,即点
,即点 到平面
到平面 的距离为
的距离为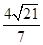 . (12分)
. (12分)
考点:(1)平行关系;(2)点面距.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
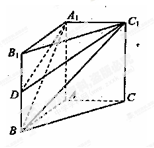
 中,
中,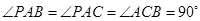 .
.
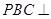 平面
平面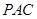 ;
;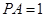 ,
,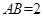 ,当三棱锥
,当三棱锥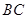 的长.
的长.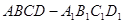 中,
中,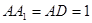 ,
,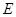 为
为 的中点,
的中点,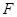 为
为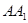 的中点.
的中点.
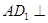 平面
平面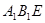 ;
;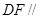 平面
平面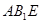 ;
;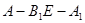 的大小为
的大小为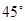 ,求
,求 的长.
的长.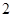 的三棱柱
的三棱柱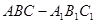 中,侧面
中,侧面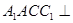 底面
底面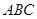 ,
,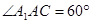 .
.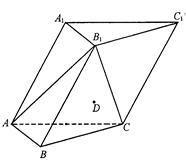
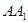 与平面
与平面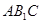 所成角的正弦值的大小;
所成角的正弦值的大小; 满足
满足 ,在直线
,在直线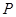 ,使
,使 ?若存在,请确定点
?若存在,请确定点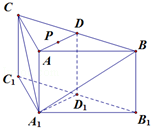
 的棱长为1,点
的棱长为1,点 分别是
分别是 和
和 的中点
的中点

 与
与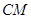 所成角的余弦值。
所成角的余弦值。 中,
中, ,
, ,
, 面
面 ,
, 为
为 的中点,
的中点, .
.
 ;
; 面
面 ;
; 的体积
的体积 .
. ,F为CE上的点,且BF
,F为CE上的点,且BF 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G