题目内容
正方形 的边长为2,
的边长为2, 分别为边
分别为边 的中点,
的中点, 是线段
是线段 的中点,如图,把正方形沿
的中点,如图,把正方形沿 折起,设
折起,设 .
.
(1)求证:无论 取何值,
取何值, 与
与 不可能垂直;
不可能垂直;
(2)设二面角 的大小为
的大小为 ,当
,当 时,求
时,求 的值.
的值.
(1) 与
与 不可能垂直; (2)
不可能垂直; (2) 的值为
的值为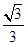 .
.
解析试题分析:(1)假设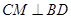 , 1分
, 1分
又因为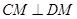 ,
,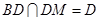 ,所以
,所以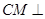 平面
平面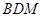 , 3分
, 3分
所以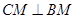 ,又
,又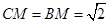 ,所以
,所以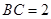 , 5分
, 5分
这与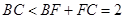 矛盾,所以假设不成立,所以
矛盾,所以假设不成立,所以 与
与 不可能垂直; 6分
不可能垂直; 6分
(2)分别以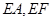 为
为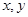 轴,过点
轴,过点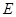 垂直平面
垂直平面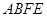 向上为
向上为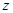 轴,如图建立坐标系,
轴,如图建立坐标系,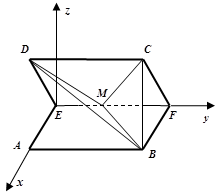
设平面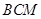 的一个法向量为
的一个法向量为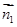 ,
,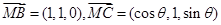 ,
,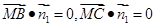 , 7分
, 7分
得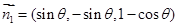 , 8分
, 8分
设平面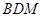 的一个法向量为
的一个法向量为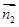 ,
,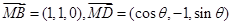 ,
,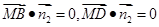 , 9分
, 9分
得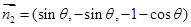 , 10分
, 10分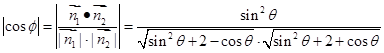 11分
11分
=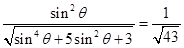 , 12分
, 12分
得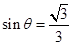 , 13分
, 13分
所以当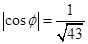 时,
时, 的值为
的值为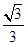 . 14分
. 14分
考点:折叠问题,平行关系,垂直关系,角的计算。
点评:中档题,立体几何问题中,平行关系、垂直关系,角、距离、面积、体积等的计算,是常见题型,基本思路是将空间问题转化成为平面问题,利用平面几何知识加以解决。要注意遵循“一作,二证,三计算”。利用“向量法”,通过建立空间直角坐标系,往往能简化解题过程。对于折叠问题,首先要弄清“变”与“不变”的几何元素。

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
 中,
中,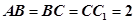 ,
, ,D是AC的中点.
,D是AC的中点.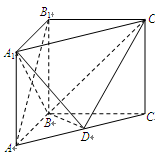
 平面
平面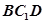 ;
;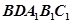 的体积.
的体积.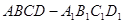 中,
中,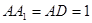 ,
,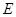 为
为 的中点,
的中点,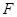 为
为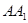 的中点.
的中点.
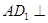 平面
平面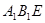 ;
;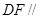 平面
平面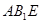 ;
;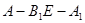 的大小为
的大小为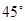 ,求
,求 的长.
的长.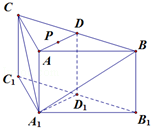
 的棱长为1,点
的棱长为1,点 分别是
分别是 和
和 的中点
的中点

 与
与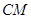 所成角的余弦值。
所成角的余弦值。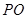 中,已知
中,已知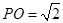 ,⊙O的直径
,⊙O的直径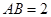 ,
,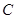 是
是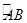 的中点,
的中点,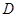 为
为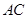 的中点.
的中点.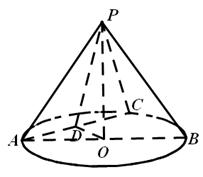
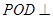 平面
平面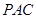 ;
;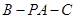 的余弦值.
的余弦值.  中,
中, ,
, ,
, 面
面 ,
, 为
为 的中点,
的中点, .
.
 ;
; 面
面 ;
; 的体积
的体积 .
.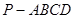 的侧面积为
的侧面积为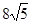 ,若
,若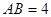 .
.
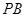 与平面
与平面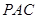 所成角的大小.
所成角的大小.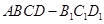 中,四边形
中,四边形 为菱形,
为菱形, ,
, ,面
,面 ∥面
∥面 、
、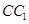 、
、 都垂直于面
都垂直于面 ,
, 为
为
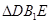 为等腰直角三角形;
为等腰直角三角形; ∥面
∥面 .
.