题目内容
3. 如图所示,在正方体ABCD-A1B1C1D1中,点M在B1C上,点N在BD上,并且MN∥平面AA1B1B,求证:CM=DN.
如图所示,在正方体ABCD-A1B1C1D1中,点M在B1C上,点N在BD上,并且MN∥平面AA1B1B,求证:CM=DN.
分析 过M作MM1⊥BB1,过N作NN1⊥AB,由于MN‖平面AA1B1B,可得MM1=NN1,通过证明三角形B1MM1和三角形BNN1全等,从而可证B1M=BN,结合B1C=BD,即可证明故CM=DN.
解答 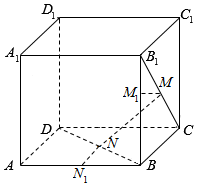 证明:过M作MM1⊥BB1,过N作NN1⊥AB,
证明:过M作MM1⊥BB1,过N作NN1⊥AB,
易证得MM1⊥面ABB1A1,NN1⊥面ABB1A1,
故MM1为M到面ABB1A1的距离,NN1为N到面ABB1A1的距离,
又由于MN‖平面AA1B1B,
所以可知MM1=NN1,
三角形B1MM1和三角形BNN1都是直角三角形,∠ABD=∠BB1C=45°,MM1=NN1,
故两三角形全等,
从而B1M=BN,
而B1C=BD,
故CM=DN.
点评 本题主要考查了线面平行的性质,三角形全等的判定和性质,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
 如图,在三棱锥V-ABC中,VB⊥平面ABC,平面VAB⊥平面VAC,则该三棱锥中共有4个直角三角形.
如图,在三棱锥V-ABC中,VB⊥平面ABC,平面VAB⊥平面VAC,则该三棱锥中共有4个直角三角形.