题目内容
18.设x>0,y>0,满足$\frac{4}{y}$+$\frac{1}{x}$=4,则x+y的最小值为( )| A. | 4 | B. | $\frac{9}{4}$ | C. | 2 | D. | 9 |
分析 根据题意,将x+y变形可得x+y=$\frac{1}{4}$×($\frac{4}{y}$+$\frac{1}{x}$)(x+y)=$\frac{1}{4}$×(5+$\frac{y}{x}$+$\frac{4x}{y}$),由基本不等式分析可得答案.
解答 解:根据题意,$\frac{4}{y}$+$\frac{1}{x}$=4,
则x+y=$\frac{1}{4}$×($\frac{4}{y}$+$\frac{1}{x}$)(x+y)=$\frac{1}{4}$×(5+$\frac{y}{x}$+$\frac{4x}{y}$)≥4×(5+2$\sqrt{\frac{y}{x}•\frac{4x}{y}}$)=$\frac{1}{4}$(5+4)=$\frac{9}{4}$,
即x+y的最小值为$\frac{9}{4}$,
故选:B.
点评 本题考查基本不等式的应用,关键是对基本不等式的灵活变形应用.

练习册系列答案
相关题目
6.若等比数列{an},前n项和Sn,且a2a3=2a1,$\frac{5}{4}$为a4与2a7的等差中项,则S4=( )
| A. | 29 | B. | 30 | C. | 31 | D. | 33 |
3. 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
| A. | 100$\sqrt{2}$米 | B. | 50($\sqrt{3}$+1)米 | C. | $100({\sqrt{3}+1})$米 | D. | 200米 |
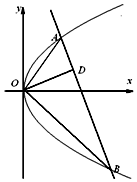 如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).