题目内容
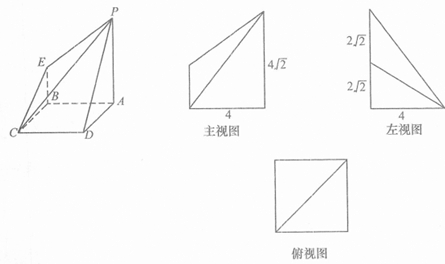
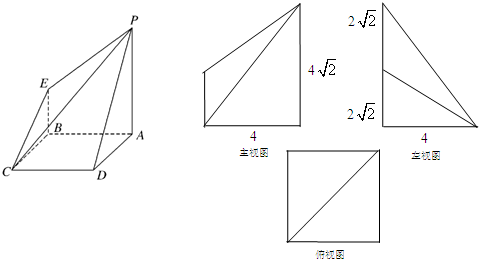
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
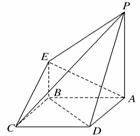
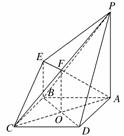
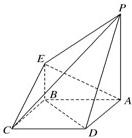
(1)求四棱锥P-ABCD的体积;
(2)证明:BD∥平面PEC;
(3)若G为BC上的动点,求证:AE⊥PG.
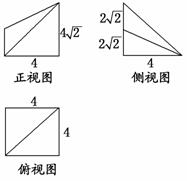
解:(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4![]() ,BE=2
,BE=2![]() ,AB=AD=CD=CB=4,
,AB=AD=CD=CB=4,
∴VP-ABCD=![]() PA×SABCD=
PA×SABCD=![]() ×4
×4![]() ×4×4=
×4×4=![]() .
.
(2)证明:连结AC交BD于O点,
取PC中点F,连结OF,
 |
∵EB∥PA,且EB=![]() PA,
PA,
又OF∥PA,且OF=![]() PA,
PA,
∴EB∥OF,且EB=OF,∴四边形EBOF为平行四边形,∴EF∥BD.
又EF⊂平面PEC,BD⊄平面PEC,所以BD∥平面PEC.
(3)连结BP,∵![]() =
=![]() =
=![]() ,∠EBA=∠BAP=90°,
,∠EBA=∠BAP=90°,
∴△EBA∽△BAP,∴∠PBA=∠BEA,∴∠PBA+∠BAE=∠BEA+∠BAE=90°,∴PB⊥AE.
又∵BC⊥平面APEB,∴BC⊥AE,∴AE⊥平面PBG,∴AE⊥PG.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).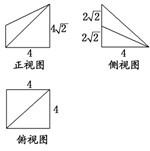
 如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积
如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积 如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为
如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为