题目内容
如图所示是一个几何体的直观图及它的三视图(其中主视图为直角梯形,俯视图为正方形,左视图为直角三角形,尺寸如图所示).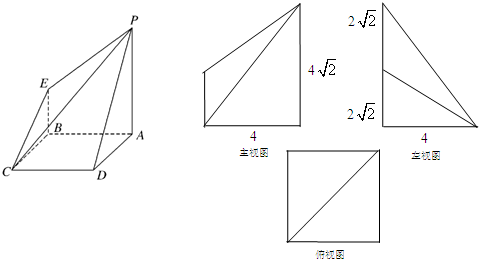
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)若G为BC的中点,求证:AE⊥PG.
分析:(I)由几何体的三视图可知,底面ABCD是边长为4的正方形,求出棱锥的高PA的长,及底面面积,代入棱锥的体积公式即可得到答案.
(II)连BP,由已知中
=
=
,∠EBA与∠BAP均为直角,我们可以得到∴△EBA∽△BAP,然后根据三角形性质,对应角相等,得到PB⊥AE,结合BC⊥AE,及线面垂直的判定定理,得到AE⊥面PBG,再由线面垂直的性质定理,即可得到答案.
(II)连BP,由已知中
| EB |
| AB |
| BA |
| PA |
| 1 | ||
|
解答:解(Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,(2分)
PA⊥面ABCD,PA∥EB,且PA=4
,BE=2
,AB=AD=CD=CB=4,(4分)
∴VP-ABCD=
PAxSABCD=
×4
×4×4=
.(5分)
(Ⅱ)连BP,∵
=
=
,∠EBA=∠BAP=90°,(7分)
∴△EBA∽△BAP,∴∠PBA=∠BEA,(8分)
∴∠PBA+∠BAE=∠BEA+∠BAE=90°,∴PB⊥AE.(10分)
又∵BC⊥面APEB,∴BC⊥AE,∴AE⊥面PBG,∴AE⊥PG.(12分)
PA⊥面ABCD,PA∥EB,且PA=4
| 2 |
| 2 |
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
64
| ||
| 3 |
(Ⅱ)连BP,∵
| EB |
| AB |
| BA |
| PA |
| 1 | ||
|
∴△EBA∽△BAP,∴∠PBA=∠BEA,(8分)
∴∠PBA+∠BAE=∠BEA+∠BAE=90°,∴PB⊥AE.(10分)
又∵BC⊥面APEB,∴BC⊥AE,∴AE⊥面PBG,∴AE⊥PG.(12分)
点评:本题考查的知识点是直线与平面垂直的性质及由三视图求体积,其中根据由几何体的三视图可知,底面ABCD是边长为4的正方形,高为PA为4
的四锥棱及其中相关的线面关系是解答本题的关键.
| 2 |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
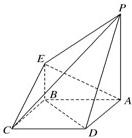 如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).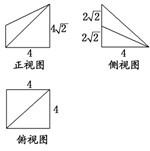
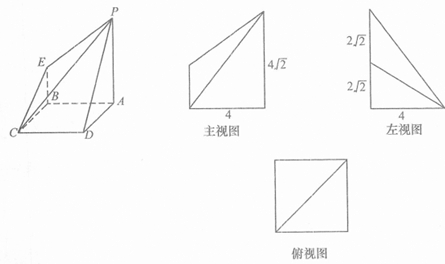
 如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积
如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积 如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为
如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为