题目内容
如图所示是一个几何体的直观图及它的三视图(其中主视图为直角梯形,俯视图为正方形,左视图为直角三角形,尺寸如图所示).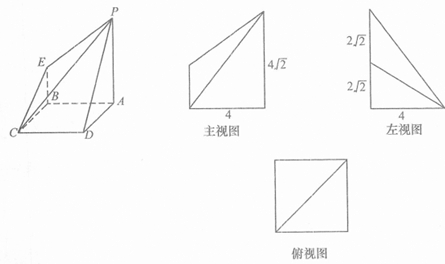
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)求二面角E-PC-D的大小.
分析:(Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,求出底面面积和高,即可求出几何体的体积.
(Ⅱ)由三视图可知,BE⊥BC,BE⊥BA,以B为原点,以BC,BA,BE所在直线分别为x,y,z轴建立空间直角坐标系,
求出平面PCD的法向量为
=(x,y,z),平面PCE的法向量为
,利用cos<
,
>=
,求出二面角E-PC-D的大小.
(Ⅱ)由三视图可知,BE⊥BC,BE⊥BA,以B为原点,以BC,BA,BE所在直线分别为x,y,z轴建立空间直角坐标系,
求出平面PCD的法向量为
| n1 |
| n2 |
| n1 |
| n2 |
| ||||
|
|
解答:解:(Ⅰ)由几何体的三视图可知,底面ABCD是边长为4的正方形,(1分)
PA⊥面ABCD,PA∥EB,且PA=4
,BE=2
,AB=AD=CD=CB=4,(3分)
∴VP-ABCD=
PA•SABCD=
×4
×4×4=
.(4分)
(Ⅱ)由三视图可知,BE⊥BC,BE⊥BA,以B为原点,以BC,BA,BE所在直线分别为x,y,z轴建立空间直角坐标系,则B(0,0,0),P(0,0,4
),D(4,4,0)C(0,4,0).(5分)
所以
=(4,0,-4
),
=(0,4,0).设平面PCD的法向量为
=(x,y,z)
,即
,取
=(
,0,1).(8分)
设平面PCE的法向量为
,同理可求
=(1,-1,
).(10分)cos<
,
>=
=
.所以二面角E-PC-D的大小为π-arccos(
).(12分)
PA⊥面ABCD,PA∥EB,且PA=4
| 2 |
| 2 |
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
64
| ||
| 3 |
(Ⅱ)由三视图可知,BE⊥BC,BE⊥BA,以B为原点,以BC,BA,BE所在直线分别为x,y,z轴建立空间直角坐标系,则B(0,0,0),P(0,0,4
| 2 |
所以
| PD |
| 2 |
| CD |
| n1 |
|
|
| n1 |
| 2 |
设平面PCE的法向量为
| n2 |
| n2 |
| 2 |
| n1 |
| n2 |
| ||||
|
|
| ||
| 3 |
| ||
| 3 |
点评:本题是中档题,考查三视图的知识,几何体的体积的求法,二面角的求法,考查计算能力,转化思想,空间想象能力的应用.

练习册系列答案
相关题目
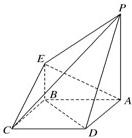 如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).
如图所示是一个几何体的直观图、正视图、俯视图、侧视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形,尺寸如图所示).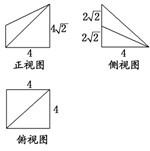
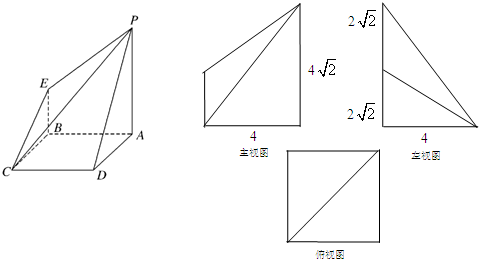
 如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积
如图所示是一个几何体的三视图(单位:cm),则这个几何体的表面积 如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为
如图所示是一个几何体的三视图,其侧视图是一个边长为a的等边三角形,俯视图是两个正三角形拼成的菱形,则该几何体的体积为