题目内容
已知函数f（x）=x2+（2a-1）x+1为偶函数，则实数a的值为 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：由函数的对称性对称2a-1=0，解出a的值即可．
解答：
解：∵函数f（x）的定义域关于原点对称，
而f（-x）=x2-（2a-1）x+1=f（x）=x2+（2a-1）x+1，
∴2a-1=0，a=
，
故答案为：
而f（-x）=x2-（2a-1）x+1=f（x）=x2+（2a-1）x+1，
∴2a-1=0，a=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了二次函数的性质，考查函数的奇偶性，是一道基础题．
练习册系列答案
相关题目
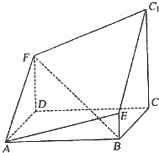如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，BC=2，CC1=3，BE=1
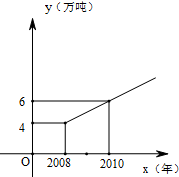某市实施“限塑令”后，2008年大约减少塑料消耗约4万吨．调查结果分析显示，从2008年开始，五年内该市因实施“限塑令”而减少的塑料消耗量y（万吨）随着时间x（年）逐年成直线上升，y与x之间的关系如图所示．