题目内容
已知
=(
sinx,cosx+sinx),
=(2cosx,sinx-cosx),f(x)=
•
.
(1)求函数f(x)的单调递增区间;
(2)当x∈[
,
]时,对任意t∈R,不等式mt2+mt+3≥f(x)恒成立,求实数的m取值范围.
| a |
| 3 |
| b |
| a |
| b |
(1)求函数f(x)的单调递增区间;
(2)当x∈[
| 5π |
| 24 |
| 5π |
| 12 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析:(1)首先根据向量的坐标运算求出函数的解析式,进一步变函数为正弦型函数,最后求出单调区间.
(2)根据函数与的定义域求出函数的值域,进一步利用恒成立问题,利用分类讨论的思想求出m的取值范围.
(2)根据函数与的定义域求出函数的值域,进一步利用恒成立问题,利用分类讨论的思想求出m的取值范围.
解答:
解:(1)已知,
=(
sinx,cosx+sinx),
=(2cosx,sinx-cosx),
则:f(x)=
•
=2
sinxcosx+(cosx+sinx)(sinx-cosx)
=
sin2x-cos2x
=2sin(2x-
),
令2kπ-
≤2x-
≤2kπ+
(k∈Z),
解得:-
+kπ≤x≤
+kπ,
所以:函数f(x)的单调递增区间为:[-
+kπ,
+kπ](k∈Z).
(2)当x∈[
,
]时,
≤2x-
≤
,
≤2sin(2x-
)≤2,
对任意t∈R,不等式mt2+mt+3≥f(x)恒成立.
只需满足:mt2+mt+3≥f(x)max成立即可.
即mt2+mt+1≥0即可.
①当m=0时,恒成立
②当m≠0时,只需满足
解得:0<m≤4
综合所得:0≤m≤4.
| a |
| 3 |
| b |
则:f(x)=
| a |
| b |
| 3 |
=
| 3 |
=2sin(2x-
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得:-
| π |
| 6 |
| π |
| 3 |
所以:函数f(x)的单调递增区间为:[-
| π |
| 6 |
| π |
| 3 |
(2)当x∈[
| 5π |
| 24 |
| 5π |
| 12 |
| π |
| 4 |
| π |
| 6 |
| 2π |
| 3 |
| 2 |
| π |
| 6 |
对任意t∈R,不等式mt2+mt+3≥f(x)恒成立.
只需满足:mt2+mt+3≥f(x)max成立即可.
即mt2+mt+1≥0即可.
①当m=0时,恒成立
②当m≠0时,只需满足
|
解得:0<m≤4
综合所得:0≤m≤4.
点评:本题考查的知识要点:三角函数关系式的恒等变换,向量的坐标运算,正弦型函数的单调区间,恒成立问题的应用.属于基础题型.

练习册系列答案
相关题目
若
,
,
均为单位向量,且
•
=0,(
+
)•
≥
2,则|
+
+
|的最小值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
| c |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
已知集合A={-1,0,1},B={x|-1<x≤1},则A∩B=( )
| A、{0} |
| B、{0,1} |
| C、{-1,0} |
| D、{-1,0,1} |
已知圆台的上下底面半径分别为1和2,高为1,则该圆台的全面积为( )
A、3
| ||||
B、(5+3
| ||||
C、
| ||||
D、
|
已知两个变量x,y具有线性相关关系,并测得(x,y)的四组值分别是(2,3)、(5,7)、(8,9)、(11,13),则求得的线性回归方程所确定的直线必定经过点( )
| A、(2,3) |
| B、(8,9) |
| C、(6,9) |
| D、(6.5,8) |
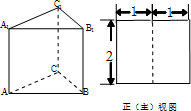 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )