题目内容
已知函数 ,
,
(1)求 在
在 处切线方程;
处切线方程;
(2)求证:函数 在区间
在区间 上单调递减;
上单调递减;
(3)若不等式 对任意的
对任意的 都成立,求实数
都成立,求实数 的最大值.
的最大值.
 ,
,(1)求
 在
在 处切线方程;
处切线方程;(2)求证:函数
 在区间
在区间 上单调递减;
上单调递减;(3)若不等式
 对任意的
对任意的 都成立,求实数
都成立,求实数 的最大值.
的最大值.(1) ;(2)详见解析;(3)
;(2)详见解析;(3)
 ;(2)详见解析;(3)
;(2)详见解析;(3)
试题分析:(1)先求导函数,再求
 ,再用点斜式方程求切线方程;(2)要证明函数
,再用点斜式方程求切线方程;(2)要证明函数 在区间
在区间 上单调递减,只需证明
上单调递减,只需证明 在
在 恒成立,先求导
恒成立,先求导 ,分母大于0,只需证明分子小于0恒成立,构造函数
,分母大于0,只需证明分子小于0恒成立,构造函数 ,说明其最大值小于0即可,这样就把问题转化为求函数的最大值问题了,继续求导
,说明其最大值小于0即可,这样就把问题转化为求函数的最大值问题了,继续求导 ,发现
,发现 ,故
,故 递减,所以
递减,所以 ;
;(3)恒成立问题可以考虑参变分离,两边取自然对数得
 ,从而参变分离为
,从而参变分离为
 ,只需用导数求右边函数的最小值即可,为了便于求导可换元,设
,只需用导数求右边函数的最小值即可,为了便于求导可换元,设
 ,则
,则
 ,进而用导数求其最小值.
,进而用导数求其最小值.试题解析:(1)由已知

 切线方程
切线方程 ;
;(2)

 ,令
,令
 =
= ,
, ,
,  在(0,1)上是减函数;
在(0,1)上是减函数;(3)

 两边取对数
两边取对数 即
即 ,令
,令
 设
设 ,设
,设 ,
, 由(2)知函数
由(2)知函数 在区间
在区间 上单调递减,
上单调递减, 在
在 上是减函数
上是减函数 ,
, 在
在 上是减函数
上是减函数 即
即 .
.
练习册系列答案
相关题目
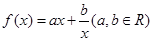 ,若
,若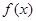 在点
在点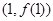 处的切线斜率为
处的切线斜率为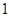 .
.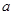 表示
表示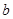 ;
;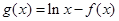 ,若
,若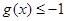 对定义域内的
对定义域内的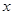 恒成立,求实数
恒成立,求实数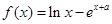 .
.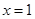 是,
是,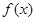 的极值点,讨论
的极值点,讨论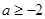 时,证明:
时,证明: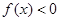 .
. .
. 的单调区间和极值;
的单调区间和极值; 直线
直线 与曲线
与曲线 相交于
相交于 不同两点,若
不同两点,若 试证明
试证明 .
. (
( 为实常数).
为实常数). 时,求函数
时,求函数 在
在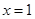 处的切线方程;
处的切线方程; .
. 的单调区间;
的单调区间; 的定义域为
的定义域为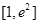 ,求函数
,求函数 的最小值
的最小值 .
. ,函数
,函数 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最小值.
上的最小值. .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. x
x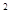 -ax+(a-1)
-ax+(a-1) ,
, 。
。 的单调性;(2)若
的单调性;(2)若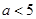 ,设
,设 ,
, ,x
,x

 ,x
,x x
x .
. ,函数
,函数
 时,求曲线
时,求曲线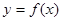 在
在 处的切线方程;
处的切线方程; 时,求函数
时,求函数 的单调区间;
的单调区间; 时,求函数
时,求函数