题目内容
10.若规定$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc(a、b∈R,a≠b),则$|\begin{array}{l}{a}&{-b}\\{b}&{a}\end{array}|$与$|\begin{array}{l}{a}&{-a}\\{b}&{b}\end{array}|$的大小关系>.(填“>”、“=”或“<”)分析 利用二阶行列式的性质和作差法求解.
解答 解:∵$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc(a、b∈R,a≠b),
∴$|\begin{array}{l}{a}&{-b}\\{b}&{a}\end{array}|$-$|\begin{array}{l}{a}&{-a}\\{b}&{b}\end{array}|$=a2+b2-ab+ab=a2+b2>0,
∴$|\begin{array}{l}{a}&{-b}\\{b}&{a}\end{array}|$>$|\begin{array}{l}{a}&{-a}\\{b}&{b}\end{array}|$.
故答案为:>.
点评 本题考查二阶行列式的大小比较,是基础题,注意作差法的合理运用.

练习册系列答案
相关题目
18.现有两个班级,每班各出4名选手进行羽毛球的男单、女单、男女混合双打(混双)比赛(注:每名选手打只打一场比赛).根据以往的比赛经验,各项目平均完成比赛所需时间如表所示,现只有一块比赛场地,各场比赛的出场顺序等可能.
(Ⅰ)求按女单、混双、男单的顺序进行比赛的概率;
(Ⅱ)求第三场比赛平均需要等待多久才能开始进行;
(Ⅲ)若要使所有参加比赛的人等待的总时间最少,应该怎样安排比赛顺序(写出结论即可).
| 比赛项目 | 男单 | 女单 | 混双 |
| 平均比赛时间 | 25分钟 | 20分钟 | 35分钟 |
(Ⅱ)求第三场比赛平均需要等待多久才能开始进行;
(Ⅲ)若要使所有参加比赛的人等待的总时间最少,应该怎样安排比赛顺序(写出结论即可).
5. 甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员成绩的标准差,$\overline{{x}_{1}}$、$\overline{{x}_{2}}$分别表示甲、乙两名运动员测试成绩的平均数,则有( )
甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员成绩的标准差,$\overline{{x}_{1}}$、$\overline{{x}_{2}}$分别表示甲、乙两名运动员测试成绩的平均数,则有( )
 甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员成绩的标准差,$\overline{{x}_{1}}$、$\overline{{x}_{2}}$分别表示甲、乙两名运动员测试成绩的平均数,则有( )
甲、乙两名运动员的5次测试成绩如图所示,设s1,s2分别表示甲、乙两名运动员成绩的标准差,$\overline{{x}_{1}}$、$\overline{{x}_{2}}$分别表示甲、乙两名运动员测试成绩的平均数,则有( )| A. | $\overline{{x}_{1}}<\overline{{x}_{2}}$,s1<s2 | B. | $\overline{{x}_{1}}>\overline{{x}_{2}}$,s1<s2 | C. | $\overline{{x}_{1}}>\overline{{x}_{2}}$,s1>s2 | D. | $\overline{{x}_{1}}<\overline{{x}_{2}}$,s1>s2 |
20.有3个大学毕业生,现在有两个工作岗位可选择,共有( )种选法.
| A. | 9 | B. | 8 | C. | 6 | D. | 5 |
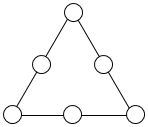 如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个.
如图,在三角形三条边上的6个不同的圆内分别填入数字1,2,3 中的一个.