题目内容
某市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于 分的有参赛资格,
分的有参赛资格, 分以下(不包括
分以下(不包括 分)的被淘汰.若有
分)的被淘汰.若有 人参加测试,学生成绩的频率分布直方图如右图所示:
人参加测试,学生成绩的频率分布直方图如右图所示:
(1)写出获得参赛资格的人数;
(2)根据频率直方图,估算这 名学生测试的平均成绩;
名学生测试的平均成绩;
(3)若知识竞赛分初赛和复赛,在初赛中每人最多有 次选题答题的机会,累计答对
次选题答题的机会,累计答对 题或答错
题或答错 题即终止,答对
题即终止,答对 题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响.已知他连续两次答错的概率为
题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响.已知他连续两次答错的概率为 ,求甲在初赛中答题个数
,求甲在初赛中答题个数 的分布列及数学期望
的分布列及数学期望 .
.

解: (Ⅰ)由频率分布直方图得,获得参赛资格的人数为500×(0.0050+0.0043+0.0032)×20=125人.
(Ⅱ)设500名学生的平均成绩为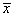 ,则
,则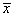 =(
=(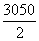 ×0.0065+
×0.0065+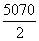 ×0.0140+
×0.0140+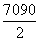 ×0.0170+
×0.0170+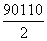 ×0.0050+
×0.0050+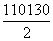 ×0.0043+
×0.0043+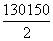 ×0.0032)×20=78.48分.
×0.0032)×20=78.48分.
(Ⅲ)设学生甲答对每道题的概率为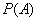 ,则
,则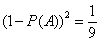 ,∴
,∴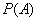 =
=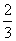 .
.
学生甲答题个数 的可能值为3,4,5,
的可能值为3,4,5,
则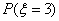 =
=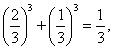
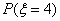 =
=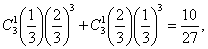
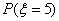 =
=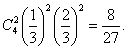 所以
所以 的分布列为
的分布列为
|
| 3 | 4 | 5 |
|
|
|
|
|
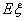 =
=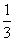 ×3+
×3+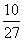 ×4+
×4+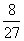 ×5=
×5=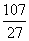 .
.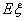 =
=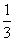 ×3+
×3+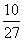 ×4+
×4+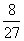 ×5=
×5=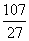 .…. (12分)
.…. (12分)

通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表:
| 空气质量 | 一级 | 二级 | 超标 |
| 日均值(微克/立方米) | 35以下 | 35~75 | 75以上 |
某城市环保局从该市城区2012年冬季每天的PM2.5监测数据中随机抽取15天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
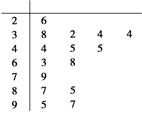
PM2.5日均值(微克/立方米)
(1)从这15天的PM2.5日均监测数据中,随机抽出三天数据,求至少有一天空气质量达到一级的概率;
(2)从这15天的数据中任取三天的数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列和数学期望.

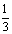
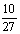
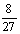
 满足
满足 ,若
,若 的最大值为
的最大值为 则
则
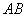 是半圆
是半圆 的直径,
的直径, 是弧
是弧 是线 段
是线 段 ,则
,则 的值是( )
的值是( )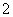 (B)
(B) (C)
(C) (D)
(D)

 满足
满足 ,若
,若 的最大值为
的最大值为 则
则
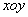 中,以坐标原点为极点,以
中,以坐标原点为极点,以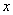 轴的非负半轴为极轴,建立极坐标系,已知直线
轴的非负半轴为极轴,建立极坐标系,已知直线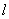 的参数方程为
的参数方程为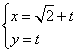 (
(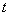 为参数),圆C的极坐标方程是
为参数),圆C的极坐标方程是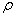 =1.
=1.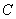 的公共点个数;
的公共点个数;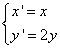 得到曲线
得到曲线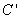 ,设
,设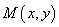 为曲线
为曲线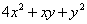 的最大值,并求相应点
的最大值,并求相应点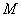 的坐标.
的坐标.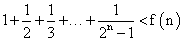 (n≥2,n∈N*)的过程,由n=k到n=k+1时,左边增加了( )
(n≥2,n∈N*)的过程,由n=k到n=k+1时,左边增加了( )
 =2
=2 ,点Q是AC的中点,若
,点Q是AC的中点,若 =(4,3),
=(4,3), =(1,5),则
=(1,5),则 =________.
=________.