题目内容
在平面直角坐标系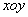 中,以坐标原点为极点,以
中,以坐标原点为极点,以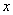 轴的非负半轴为极轴,建立极坐标系,已知直线
轴的非负半轴为极轴,建立极坐标系,已知直线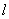 的参数方程为
的参数方程为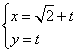 (
(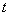 为参数),圆C的极坐标方程是
为参数),圆C的极坐标方程是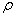 =1.
=1.
(1)求直线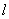 与圆
与圆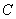 的公共点个数;
的公共点个数;
(2)在平面直角坐标系中,圆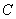 经过伸缩变换
经过伸缩变换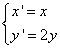 得到曲线
得到曲线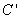 ,设
,设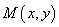 为曲线
为曲线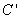 上一点,求
上一点,求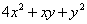 的最大值,并求相应点
的最大值,并求相应点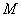 的坐标.
的坐标.
(Ⅰ)直线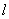 的方程为
的方程为 圆
圆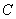 的方程是
的方程是
圆心到直线的距离为 ,等于圆半径,∴直线
,等于圆半径,∴直线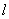 与圆
与圆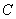 的公共点个数为
的公共点个数为 ;
;
(Ⅱ)圆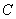 的参数方程方程是
的参数方程方程是 ∴曲线
∴曲线 的参数方程是
的参数方程是
∴
当 或
或 时,
时, 取得最大值
取得最大值
此时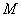 的坐标为
的坐标为 或
或

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
今年春节黄金周,记者通过随机询问某景区110名游客对景区的服务是否满意,得到如下的列联表:性别与对景区的服务是否满意(单位:名).
| 男 | 女 | 总计 | |
| 满意 | 50 | 30 | 80 |
| 不满意 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
(I)从这50名女游客中按对景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,问样本中满意与不满意的女游客各有多少名?
(II)从(1)中的5名女游客样本中随机选取两名作深度访谈,求选到满意与不满意的女游客各一名的概率;
(Ⅲ)根据以上列联表,在犯错误不超过多少的情况下认为“游客性别与对景区的服务满意”有关
|
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 |
 ,
, ,则
,则 ( )
( ) B.
B. C.
C.  D.
D.


 ,
, 两点(
两点(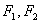 为双曲线的两个焦点,则
为双曲线的两个焦点,则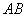 的垂直平分线上
的垂直平分线上  分的有参赛资格,
分的有参赛资格, 人参加测试,学生成绩的频率分布直方图如右图所示:
人参加测试,学生成绩的频率分布直方图如右图所示: 题或答错
题或答错 ,求甲在初赛中答题个数
,求甲在初赛中答题个数 的分布列及数学期望
的分布列及数学期望 .
.
 ,n是正整数,假设n=k时,等式成立,则当n=k+1时,应推证的目标等式是_____________.
,n是正整数,假设n=k时,等式成立,则当n=k+1时,应推证的目标等式是_____________. =3
=3 ,点O在线段CD上(与点C、D不重合),若
,点O在线段CD上(与点C、D不重合),若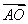 =x
=x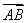 +(1-x)
+(1-x)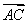 ,则x的取值范围是( )
,则x的取值范围是( )