题目内容
（文科）已知等差数列{an}中，a4=4，a8=8，则该数列的前11项的和S11=（ ）
| A、77 | B、66 | C、55 | D、121 |
考点：等差数列的前n项和
专题：计算题,等差数列与等比数列
分析：根据等差数列的性质以及前n项和公式，即可求出该数列的前11项和．
解答：
解：等差数列{an}中，∵a4=4，a8=8，
∴a1+a11=a4+a8=4+8=12；
∴该数列的前11项的和
S11=
=
=66．
故选：B．
∴a1+a11=a4+a8=4+8=12；
∴该数列的前11项的和
S11=
| 11(a1+a11) |
| 2 |
| 11×12 |
| 2 |
故选：B．
点评：本题考查了等差数列的性质以及前n项和公式的应用问题，也考查了一定的计算能力，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
下列各式中，正确的是（ ）
| A、（z1-z2）2+（z2-z3）2=0?z1=z2=z3 | ||||
B、|z|=1?z=
| ||||
| C、|z1+z2|=|z1|+|z2| | ||||
| D、|z|2=z2 |
（文科）已知F1、F2是椭圆
+
=1（a＞b＞0）的两个焦点，若椭圆上存在点P，满足∠F1PF2=120°，则
的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| b |
A、（
| ||
B、（
| ||
C、[
| ||
D、（1，
|
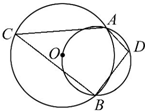如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C，D分别在两圆上，若∠ADB=100°，则∠ACB的度数为（ ）| A、35° | B、40° |
| C、50° | D、80° |
已知A（3，1），B（2，-1），则
的坐标是（ ）
| BA |
| A、（-2，-1） |
| B、（2，1） |
| C、（1，2） |
| D、（-1，-2） |
在平面直角坐标系中，设M（-3，2）、N（2，-3），沿x轴把坐标平面折成90°的二面角后，则|
|的长为（ ）
| MN |
A、
| ||
B、
| ||
C、2
| ||
D、5
|
已知直线的点斜式方程是-3y-2=
（x-1），那么此直线的倾斜角为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）=x3-2cx2+x有极值点，则实数c的范围为（ ）
A、[
| ||||||||
B、（
| ||||||||
C、（-∞，-
| ||||||||
D、（-∞，-
|
下表显示出函数值y随自变量x变化的一组数据，由此判断符合这组数据的最恰当的函数模型是（ ）
| x | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
| y | … | 13 | 15 | 17 | 19 | 21 | 23 | 25 | … |
| A、一次函数模型 |
| B、二次函数模型 |
| C、指数函数模型 |
| D、对数函数模型 |