题目内容
已知椭圆C: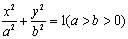 ,经过点
,经过点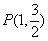 ,离心率
,离心率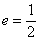 ,直线
,直线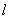 的方程为
的方程为 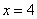 .
.
(1)求椭圆C的方程;
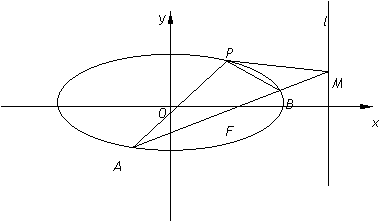 (2)AB是经过右焦点F的任一弦(不经过点P),设直线l与直线AB相交于点M,记PA、PB、PM的斜率分别为
(2)AB是经过右焦点F的任一弦(不经过点P),设直线l与直线AB相交于点M,记PA、PB、PM的斜率分别为 ,问:是否存在常数
,问:是否存在常数 ,使得
,使得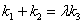 ?若存在,求出
?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(1)由点 在
在 椭圆上得,
椭圆上得, ①
① ②
②
由 ①②得 ,故椭圆
,故椭圆 的方程为
的方程为 .......4分
.......4分
(2)假设存在常数 ,使得
,使得 .
.
由题意可设
 ③
③
代入椭圆方程 并整理得
并整理得
设 ,则有
,则有 ④......6分
④......6分
在方程③中,令 得,
得, ,从而
,从而
 .又因为
.又因为 共线,则有
共线,则有 ,
,
即有
所以


=
 ⑤
⑤
将④代入⑤得

 ,又
,又 ,
,
所以

故存在常数 符合题意......12分
符合题意......12分

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 是边长为
是边长为 的正方形,
的正方形, 平面
平面 ,
, 且
且 .
. ∥平面
∥平面 ;
; 平面
平面

 ,其中
,其中 表示不超过实数
表示不超过实数 的最大整数,如
的最大整数,如 .若
.若 ,则
,则 的值域为 .
的值域为 . 与椭圆C2
与椭圆C2 B.
B. C.
C. D.
D.

 被圆
被圆 截得的弦长为4
截得的弦长为4 的最小值是
的最小值是  的值是
的值是 (C)
(C) (D)
(D)
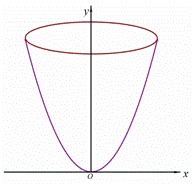
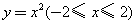 绕
绕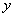 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是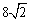 (D)
(D)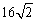
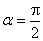 ”是“
”是“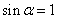 ”的充要条件;
”的充要条件; 的展开式中的常数项为
的展开式中的常数项为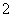 ;
;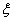 ~
~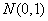 ,若
,若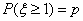 ,则
,则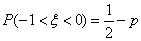 .
. ”是“关于
”是“关于 的不等式组
的不等式组 表示的平面区域为三角形”的
表示的平面区域为三角形”的 必要条件
必要条件  B. 必要不充分条件
B. 必要不充分条件