题目内容
(本小题满分12分) 已知数列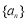 是递增的等差数列,
是递增的等差数列,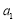 ,
,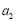 是方程
是方程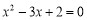 的两根.
的两根.
(Ⅰ)求数列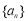 的通项公式;
的通项公式;
(Ⅱ)求数列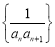 的前
的前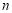 项和
项和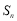 .
.
(Ⅰ) ; (Ⅱ)
; (Ⅱ) .
.
【解析】
试题分析:(Ⅰ)方程 的两根为1,2,由题意得
的两根为1,2,由题意得 ,
, ,设数列
,设数列 的公差为
的公差为 ,则
,则 ,根据等差数列的通项公式即可求出数列
,根据等差数列的通项公式即可求出数列 的通项公式;(Ⅱ)由(Ⅰ)知
的通项公式;(Ⅱ)由(Ⅰ)知 ,利用裂项相消即可求和.
,利用裂项相消即可求和.
试题解析:【解析】
(Ⅰ)方程 的两根为1,2,由题意得
的两根为1,2,由题意得 ,
, . 2分
. 2分
设数列 的公差为
的公差为 ,则
,则 , 4分
, 4分
所以数列 的通项公式为
的通项公式为 . 6分
. 6分
(Ⅱ)由(Ⅰ)知 , 8分
, 8分
所以
 10分
10分
 . 12分
. 12分
考点:1.等差数列的通项公式、裂项相消法求数列的和.

练习册系列答案
相关题目
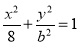 (b > 0),点G(2,0),点P在椭圆上,且PG⊥x轴,连接OP交直线x = 4于点M,连接MG交椭圆于A、B.
(b > 0),点G(2,0),点P在椭圆上,且PG⊥x轴,连接OP交直线x = 4于点M,连接MG交椭圆于A、B.
 ,
,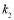 ,求
,求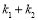 的取值范围.
的取值范围. 的模为
的模为 ,则实数
,则实数 的值为
的值为 C.
C. D.
D.
 若z=y-ax取得最大值的最优解不唯一,则实数a的值为
若z=y-ax取得最大值的最优解不唯一,则实数a的值为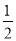 或-1 B.2或
或-1 B.2或 C.2或1 D.2或-1
C.2或1 D.2或-1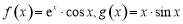 ,其中
,其中 为自然对数的底数.
为自然对数的底数.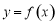 在点
在点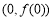 处的切线方程;
处的切线方程; ,不等式
,不等式 恒成立,求实数
恒成立,求实数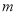 的取值范围;
的取值范围; 时,方程
时,方程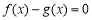 解的个数,并说明理由.
解的个数,并说明理由.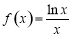 ,有下列四个命题:
,有下列四个命题: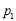 :
: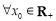 ,
, ,
,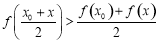 ;
; :
: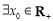 ,
,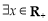 ,
, ;
;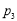 :
: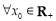 ,
,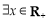 ,
, ;
;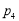 :
: ,
,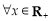 ,
, .
.
 B.
B. C.
C. D.
D.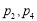
 ”是“
”是“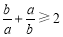 ”的( ).
”的( ). ”为:
”为: .若函数
.若函数 ,则该函数的图象大致是( ).
,则该函数的图象大致是( ).
 中,
中, 是
是 的中点,点
的中点,点 是面
是面 所在的平面内的动点,且满足
所在的平面内的动点,且满足 ,则点
,则点