题目内容
(本小题满分13分)如图,焦点在x轴的椭圆C: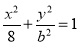 (b > 0),点G(2,0),点P在椭圆上,且PG⊥x轴,连接OP交直线x = 4于点M,连接MG交椭圆于A、B.
(b > 0),点G(2,0),点P在椭圆上,且PG⊥x轴,连接OP交直线x = 4于点M,连接MG交椭圆于A、B.

(Ⅰ)若G为椭圆右焦点,求|OM|;
(Ⅱ)记直线PA,PB的斜率分别为 ,
,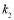 ,求
,求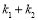 的取值范围.
的取值范围.
(Ⅰ)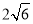 (Ⅱ)
(Ⅱ)
【解析】
试题分析:(Ⅰ)因为点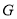 是椭圆的右焦点,所以可得
是椭圆的右焦点,所以可得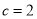 ,所以
,所以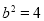 ,求出点
,求出点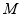 坐标,由距离公式求之即可. (Ⅱ)由
坐标,由距离公式求之即可. (Ⅱ)由 四点共线可得
四点共线可得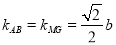 ,设出直线
,设出直线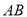 的方程,与椭圆方程联立,由韦达定理求出
的方程,与椭圆方程联立,由韦达定理求出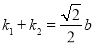 ,可求范围.
,可求范围.
试题解析:解:不妨设P在x轴上方,因为椭圆C的方程为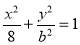 ,令x=2,则
,令x=2,则 ,
,
所以点P的坐标为 ,
,
根据题意可得P为线段OM的中点,所以M的坐标为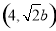 .
.
(Ⅰ)若G为椭圆右焦点,则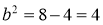 ,
,
所以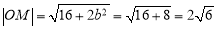 5分
5分
(Ⅱ)因为直线AB过点M、G,所以AB的斜率为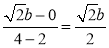 ,
,
则直线AB的方程为  ① 7分
① 7分
代入椭圆方程 并整理得:
并整理得: . 8分
. 8分
设 ,
,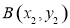 ,则由韦达定理有
,则由韦达定理有
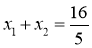 ,
,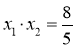 ②
②
所以,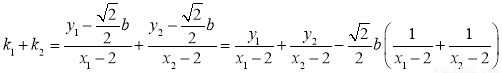 .
.
因为直线AB的方程为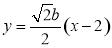 ,所以
,所以 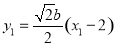 ,
,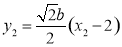
所以 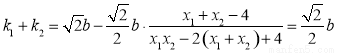 ③ 12分
③ 12分
因为 ,
, ,所以
,所以 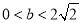 ,
,
所以, 的取值范围是
的取值范围是 13分
13分
考点:椭圆的几何性质、直线与圆锥曲线的位置关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 与双曲线
与双曲线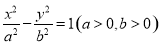 有相同的焦点
有相同的焦点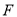 ,点
,点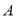 是两曲线的一个交点,且
是两曲线的一个交点,且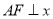 轴,则双曲线的离心率为 .
轴,则双曲线的离心率为 .  ,B=
,B= 求:
求: ,
, 

 ,则
,则 的大小关系是( )
的大小关系是( ) B.
B.  C.
C.  D.
D. 
 的图像不经过第四象限,则函数
的图像不经过第四象限,则函数 的值域为
的值域为  的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。若直线PA、PB的倾斜角分别为α、β,且
的左、右顶点分别为A、B,点P是第一象限内双曲线上的点。若直线PA、PB的倾斜角分别为α、β,且 ,那么α的值是( )
,那么α的值是( ) B.
B. C.
C.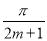 D.
D.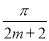
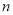 的值为100,则输出S的值为_______.
的值为100,则输出S的值为_______.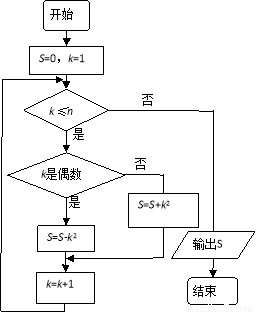
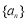 是递增的等差数列,
是递增的等差数列,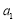 ,
,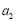 是方程
是方程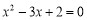 的两根.
的两根.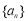 的通项公式;
的通项公式;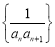 的前
的前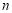 项和
项和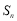 .
.