题目内容
(1)已知a,b∈R,求证:a2+b2≥ab+a+b-1.
(2)已知|a|<1,|b|<1,求证:|1-ab|>|a-b|.
(2)已知|a|<1,|b|<1,求证:|1-ab|>|a-b|.
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:(1)欲证明a2+b2≥ab+a+b-1,利用比较法,只须证明 (a2+b2)-(ab+a+b-1)>0即可,故先作差后因式分解后与0比较即可;
(2)首先化简|1-ab|2-|a-b|2可得,|1-ab|2-|a-b|2=1+a2b2-a2-b2=(a2-1)(b2-1);结合题意中|a|<1,|b|<1,可得a、b的范围,进而可得|1-ab|2-|a-b|2>0,由不等式的性质,可得答案.
(2)首先化简|1-ab|2-|a-b|2可得,|1-ab|2-|a-b|2=1+a2b2-a2-b2=(a2-1)(b2-1);结合题意中|a|<1,|b|<1,可得a、b的范围,进而可得|1-ab|2-|a-b|2>0,由不等式的性质,可得答案.
解答:
证明:(1)(a2+b2)-(ab+a+b-1)
=
(2a2+2b2-2ab-2a-2b+2)
=
[(a2-2ab+b2)+(a2-2a+1)+(b2-2b+1)]
=
[(a-b)2+(a-1)2+(b-1)2]≥0,
则a2+b2≥ab+a+b-1;
(2)|1-ab|2-|a-b|2=1+a2b2-a2-b2=(a2-1)(b2-1).
由于|a|<1,|b|<1,则a2-1<0,b2-1<0.
则|1-ab|2-|a-b|2>0,
故有|1-ab|>|a-b|.
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
则a2+b2≥ab+a+b-1;
(2)|1-ab|2-|a-b|2=1+a2b2-a2-b2=(a2-1)(b2-1).
由于|a|<1,|b|<1,则a2-1<0,b2-1<0.
则|1-ab|2-|a-b|2>0,
故有|1-ab|>|a-b|.
点评:本题考查不等式的证明,考查比较法的运用以及不等式性质的基本运用,注意结合题意,进行绝对值的转化,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
若函数f(x)=-
x2+bx+1在[-1,+∞)上是减函数,则b的取值范围是( )
| 1 |
| 2 |
| A、[-1,+∞) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、(-∞,-1] |
下列四个函数中,在(0,+∞)上为增函数的是( )
| A、f(x)=3-x | ||
| B、f(x)=x2-3x | ||
| C、f(x)=2x | ||
D、f(x)=
|
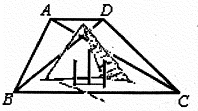 如图,在一座底部不可到达的孤山两侧,有两段平行的公路AB和CD,现测得AB=5,AC=9∠BCA=30°,∠ADB=45°
如图,在一座底部不可到达的孤山两侧,有两段平行的公路AB和CD,现测得AB=5,AC=9∠BCA=30°,∠ADB=45°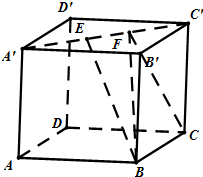 如图,正方体ABCD-A′B′C′D′的棱线长为1,线段AC′上有两个动点E,F,且EF=
如图,正方体ABCD-A′B′C′D′的棱线长为1,线段AC′上有两个动点E,F,且EF=