题目内容
2.多次执行如图所示的程序框图,输出的$\frac{m}{n}$的值会稳定在某个常数附近,则这个常数为( )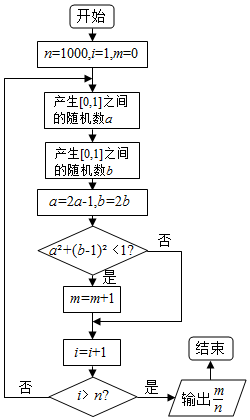
| A. | $\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{16}$ |
分析 根据已知中的流程图我们可以得到该程序的功能是利用随机模拟实验的方法求任取[0,1]上的两个数a,b,求(a-$\frac{1}{2}$)2+(b-$\frac{1}{2}$)2<$\frac{1}{4}$的概率,然后利用几何概型的概率公式解之即可.
解答 解:根据已知中的流程图我们可以得到:
该程序的功能是利用随机模拟实验的方法求任取[0,1]上的两个数a,b,
求(2a-1)2+(2b-1)2<1,即:(a-$\frac{1}{2}$)2+(b-$\frac{1}{2}$)2<$\frac{1}{4}$的概率,
由于,a∈[0,1],b∈[0,1],(a-$\frac{1}{2}$)2+(b-$\frac{1}{2}$)2<$\frac{1}{4}$对应的平面区域的面积为图形中阴影部分面积:
故P=$\frac{π×(\frac{1}{2})^{2}}{1×1}$=$\frac{π}{4}$.
故选:A.
点评 本题主要考查了循环结构,其中根据已知中的程序流程图分析出程序的功能,并将问题转化为几何概型问题是解答本题的关键,属于基础题.

练习册系列答案
相关题目
13.已知t>0,函数f(x)=2x-1+$\sqrt{4+t-2tx}$的最大值为g(t),则g(t)的最小值为( )
| A. | 2 | B. | $\frac{\sqrt{2}}{4}$ | C. | 1 | D. | 2$\sqrt{2}$ |
17.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{3}x|\\;0<x<3}\\{sin(\frac{π}{6}x)\\;3≤x≤15}\end{array}\right.$,若存在实数x1,x2,x3,x4满足f(x1)=f(x2)=f(x3)=f(x4),其中x1<x2<x3<x4,则x1x2x3x4取值范围是( )
| A. | (60,96) | B. | (45,72) | C. | (30,48) | D. | (15,24) |
7.下列函数中,有最小正周期的是( )
| A. | y=sin|x| | B. | y=cos|x| | C. | y=tan|x| | D. | y=(x2+1)0 |
12.电流I随时间t变化的函数关系式为I=5sin(100πt+$\frac{π}{3}$),t∈[0,+∞),则初相为( )
| A. | 5 | B. | $\frac{1}{50}$ | C. | $\frac{π}{3}$ | D. | 100πt+$\frac{π}{3}$ |