题目内容

11．函数f（x）的图象如图所示，则函数f（x）的解析式是f（x）=$\left\{\begin{array}{l}{丨x-2丨}&{x≥0}\\{丨x+2丨}&{x＜0}\end{array}\right.$．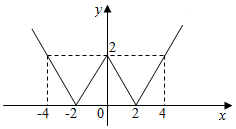

分析 观察分段函数的图象的形状，分别写出x≥0及x＜0的解析式．

解答 解：由函数的图象关于y轴对称，
当x≥0，f（x）=丨x-2丨，
当x＜0，f（x）=丨x+2丨，
∴函数f（x）的解析式是f（x）=$\left\{\begin{array}{l}{丨x-2丨}&{x≥0}\\{丨x+2丨}&{x＜0}\end{array}\right.$．
故答案为f（x）=$\left\{\begin{array}{l}{丨x-2丨}&{x≥0}\\{丨x+2丨}&{x＜0}\end{array}\right.$．

点评 本题考查学生观察图象的能力，并根据图象写出分段函数的解析式，属于基础题．

练习册系列答案
相关题目
1．在直角坐标系xOy中，已知点A（0，1），点B（-3，4），若点C在∠AOB的平分线上，则向量$\overrightarrow{OC}$可以等于（　　）
A．（-2，3）B．（-2，4）C．（-1，4）D．（-1，3）
2．多次执行如图所示的程序框图，输出的$\frac{m}{n}$的值会稳定在某个常数附近，则这个常数为（　　）
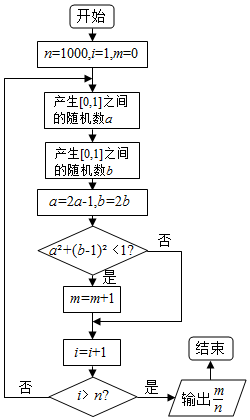
A．$\frac{π}{4}$B．$\frac{π}{6}$C．$\frac{π}{8}$D．$\frac{π}{16}$
19．已知各项均为正数的数列{an}，其前n项和为Sn，且Sn，an，$\frac{1}{2}$成等差数列，则数列{an}的通项公式为（　　）
A．2n-3B．2n-2C．2n-1D．2n-2+1
6．执行如图的程序框图，若输入M的值为1，则输出的S=（　　）
A．6B．12C．14D．20
16．已知数列{an}满足a1=1，且an+1=an+$\frac{{a}_{n}+{n}^{2}+n}{n}$．
（1）证明：数列{$\frac{{a}_{n}}{n}$}为等差数列；
（2）若数列{bn}满足anbn=2nn2-n3，求数列{bn}的前n项和Sn．
3．已知函数f（x）=$\left\{\begin{array}{l}{\frac{2{x}^{2}}{x+1}，x∈（\frac{1}{2}，1]}\\{-\frac{1}{3}x+\frac{1}{6}，x∈[0，\frac{1}{2}]}\end{array}\right.$，g（x）=$\frac{1}{2}$ax2-2a+2（a＞0），若存在x1，x2∈[0，1]，使得f（x1）=g（x2）成立，则实数a的取值范围是$\frac{1}{2}$≤a≤$\frac{4}{3}$．
20．已知函数f（x）=asin（πx+θ）+bcos（πx+θ）+x，且f（2006）=2005，则f（2007）的值为（　　）
A．2005B．2006C．2007D．2008
1．在△ABC中，内角A，B，C所对的边分别是a，b，c，（a+b+c）（b+c-a）=3bc，a=$\sqrt{3}$，tanB=$\frac{\sqrt{2}}{4}$，则b的值为$\frac{2}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网