题目内容
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,给出下列三个叙述:
,给出下列三个叙述:
①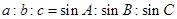
②
③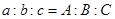
以上三个叙述中能作为“ 是等边三角形”的充分必要条件的个数为( )
是等边三角形”的充分必要条件的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
C
解析试题分析:根据正弦定理,无论是何三角形都有①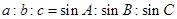 ,即不能作为“
,即不能作为“ 是等边三角形”的充分必要条件;
是等边三角形”的充分必要条件;
而由正弦定理 ,且
,且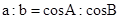 ,
,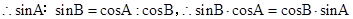 ,所以, sin(B-A)=0,因而,
,所以, sin(B-A)=0,因而,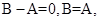 同理可得
同理可得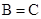 ,得三角形ABC是等边三角形. ②
,得三角形ABC是等边三角形. ② 能作为“
能作为“ 是等边三角形”的充分必要条件;
是等边三角形”的充分必要条件;
由正弦定理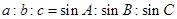 及条件
及条件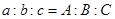 ,得,
,得,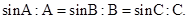
构造函数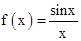 ,
, 则
则 ,
, 时,总有
时,总有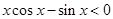 ,
,
故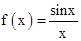 在
在 是单调减函数,所以,A="B=C" , 从而三角形是正三角形,即③
是单调减函数,所以,A="B=C" , 从而三角形是正三角形,即③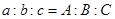 能作为“
能作为“ 是等边三角形”的充分必要条件.故选C.
是等边三角形”的充分必要条件.故选C.
考点:正弦定理的应用,充要条件,应用导数研究函数的单调性.

练习册系列答案
相关题目
若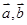 为平面向量,则“
为平面向量,则“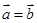 ”是“
”是“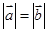 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“数列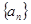 为常数列”是“数列
为常数列”是“数列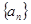 既是等差数列又是等比数列”的( )
既是等差数列又是等比数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出命题:已知 为实数,若
为实数,若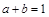 ,则
,则 .在它的逆命题、否命题、逆否命三个命题中,假命题的个数是( )
.在它的逆命题、否命题、逆否命三个命题中,假命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |
命题 :对任意
:对任意 ,
,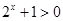 的否定是( )
的否定是( )
A.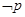 :存在 :存在 , ,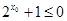 | B.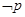 :存在 :存在 , ,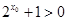 |
C.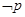 :不存在 :不存在 , ,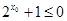 | D.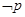 :对任意 :对任意 , , |
已知命题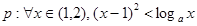 恒成立;命题
恒成立;命题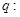 方程
方程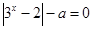 有两个实数根,则命题
有两个实数根,则命题 是命题
是命题 成立的( )条件
成立的( )条件
| A.充分而不必要 | B.必要而不充分 |
| C.充要 | D.既不充分也不必要 |
“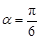 ”是“
”是“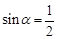 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
4. 下列命题中的假命题是( )
A.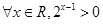 | B.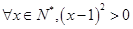 |
C.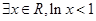 | D.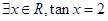 |
已知条件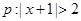 ,条件
,条件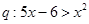 ,则
,则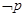 是
是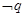 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |