题目内容
已知条件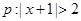 ,条件
,条件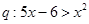 ,则
,则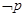 是
是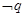 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 | C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:由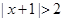 ,得
,得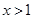 或
或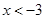 ,所以由
,所以由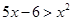 ,得
,得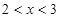 ,所以
,所以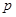 是
是 的必要不充分条件,于是
的必要不充分条件,于是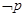 是
是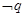 的充分不必要条件,选A.
的充分不必要条件,选A.
考点:充分条件和必要条件、解不等式.

练习册系列答案
相关题目
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,给出下列三个叙述:
,给出下列三个叙述:
①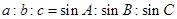
②
③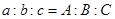
以上三个叙述中能作为“ 是等边三角形”的充分必要条件的个数为( )
是等边三角形”的充分必要条件的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
若“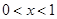 ”是“
”是“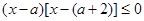 ”的充分不必要条件,则实数
”的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A.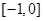 | B.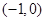 |
C.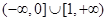 | D.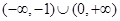 |
已知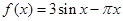 ,命题
,命题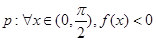 ,则( )
,则( )
A.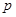 是假命题; 是假命题; |
B.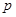 是假命题; 是假命题;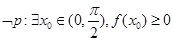 |
C.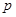 是真命题; 是真命题;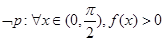 |
D.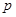 是真命题 是真命题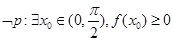 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给定下列两个命题:
①“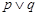 ”为真是“
”为真是“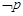 ”为假的必要不充分条件;
”为假的必要不充分条件;
②“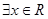 ,使
,使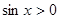 ”的否定是“
”的否定是“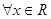 ,使
,使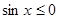 ”.其中说法正确的是( )
”.其中说法正确的是( )
| A.①真②假 | B.①假②真 | C.①和②都为假 | D.①和②都为真 |
下列有关命题的说法正确的是 ( )
A.命题“若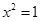 ,则 ,则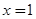 ”的否命题为:“若 ”的否命题为:“若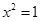 ,则 ,则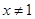 ”. ”. |
B.“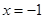 ”是“ ”是“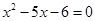 ”的必要不充分条件. ”的必要不充分条件. |
C.命题“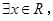 使得 使得 ”的否定是:“ ”的否定是:“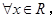 均有 均有 ”. ”. |
D.命题“若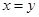 ,则 ,则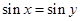 ”的逆否命题为真命题. ”的逆否命题为真命题. |
下列说法错误的是( )
A.若命题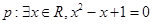 ,则 ,则 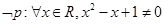 ; ; |
B.“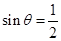 ”是“ ”是“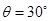 ”的充分不必要条件; ”的充分不必要条件; |
C.命题“若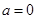 ,则 ,则 ”的否命题是:“若 ”的否命题是:“若 ,则 ,则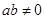 ”; ”; |
D.已知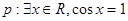 , ,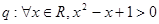 ,则“ ,则“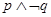 ”为假命题. ”为假命题. |
用反证法证明命题:若整数系数的一元二次方程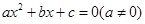 有有理实数根,那么
有有理实数根,那么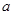 ,
,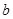 ,
,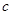 中至少有一个是偶数,下列假设中正确的是( )
中至少有一个是偶数,下列假设中正确的是( )
A.假设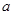 , ,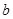 , ,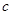 至多有一个是偶数 至多有一个是偶数 |
B.假设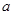 , ,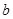 , ,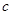 至多有两个偶数 至多有两个偶数 |
C.假设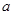 , ,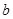 , ,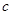 都是偶数 都是偶数 |
D.假设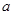 , ,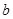 , ,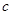 都不是偶数 都不是偶数 |