题目内容
若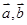 为平面向量,则“
为平面向量,则“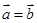 ”是“
”是“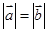 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:若“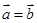 ”则“
”则“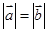 ”,反之“
”,反之“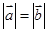 ”,当
”,当 时,
时, ,故“
,故“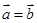 ”是“
”是“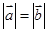 ”的充分不必要条件.
”的充分不必要条件.
考点:充要条件的判断.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
命题 的否定为( )
的否定为( )
A. | B. |
C. | D. |
“ ”方程“
”方程“ 表示双曲线”的( )
表示双曲线”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.既不充分也不必要条件 | D.充分必要条件 |
“△ 的三个角A,B,C成等差数列”是“△
的三个角A,B,C成等差数列”是“△ 为等边三角形”的( )
为等边三角形”的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列有关命题的说法正确的是 ( )
A.命题“若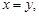 则 则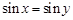 ”的逆否命题为真命题. ”的逆否命题为真命题. |
B.函数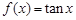 的定义域为 的定义域为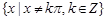 . . |
C.命题“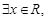 使得 使得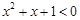 ”的否定是:“ ”的否定是:“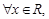 均有 均有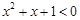 ” . ” . |
D.“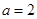 ”是“直线 ”是“直线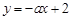 与 与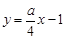 垂直”的必要不充分条件. 垂直”的必要不充分条件. |
设 ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知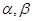 为不重合的两个平面,直线
为不重合的两个平面,直线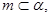 那么“
那么“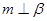 ”是“
”是“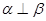 ”的( )
”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
有下述命题
①若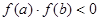 ,则函数
,则函数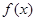 在
在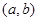 内必有零点;
内必有零点;
②当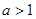 时,总存在
时,总存在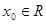 ,当
,当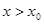 时,总有
时,总有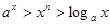 ;
;
③函数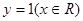 是幂函数;
是幂函数;
④若
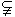
 ,则
,则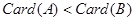 其中真命题的个数是( )
其中真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,给出下列三个叙述:
,给出下列三个叙述:
①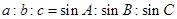
②
③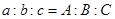
以上三个叙述中能作为“ 是等边三角形”的充分必要条件的个数为( )
是等边三角形”的充分必要条件的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |