题目内容
“数列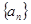 为常数列”是“数列
为常数列”是“数列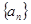 既是等差数列又是等比数列”的( )
既是等差数列又是等比数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:数列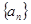 为常数列,如果
为常数列,如果 ,则数列
,则数列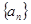 不是等比数列;
不是等比数列;
显然数列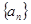 是以
是以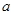 为首项,以0为公差的等差数列,且
为首项,以0为公差的等差数列,且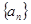 是以
是以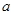 为首项,以1为公比的等比数列.
为首项,以1为公比的等比数列.
若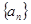 既是等差数列又是等比数列,则对任意
既是等差数列又是等比数列,则对任意 都有:
都有:
可得 ,整理得
,整理得 ,∴
,∴ .
.
∴{an}是常数列.
∴“数列{an}既是等差数列又是等比数列”⇒数列{an}为常数列”
∴“数列{an}为常数列”是“数列{an}既是等差数列又是等比数列”的必要不充分条件,
故选B;
考点:充要条件,等差数列,等比数列.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
“ ”方程“
”方程“ 表示双曲线”的( )
表示双曲线”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.既不充分也不必要条件 | D.充分必要条件 |
已知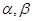 为不重合的两个平面,直线
为不重合的两个平面,直线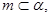 那么“
那么“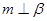 ”是“
”是“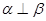 ”的( )
”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
有下述命题
①若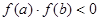 ,则函数
,则函数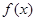 在
在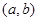 内必有零点;
内必有零点;
②当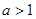 时,总存在
时,总存在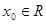 ,当
,当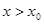 时,总有
时,总有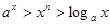 ;
;
③函数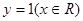 是幂函数;
是幂函数;
④若
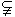
 ,则
,则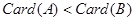 其中真命题的个数是( )
其中真命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
设 分别为两个不同的平面,直线
分别为两个不同的平面,直线 ,则“
,则“ ”是“
”是“ ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
两个非零向量 的夹角为
的夹角为 ,则“
,则“ ”是“
”是“ 为锐角”的( )
为锐角”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
命题“存在 使得
使得 ”的否定是( )
”的否定是( )
A.不存在 使得 使得 | B.对任意 , , |
C.对任意 , , | D.存在 ,使得 ,使得 |
 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,给出下列三个叙述:
,给出下列三个叙述:
①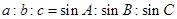
②
③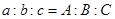
以上三个叙述中能作为“ 是等边三角形”的充分必要条件的个数为( )
是等边三角形”的充分必要条件的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
若“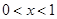 ”是“
”是“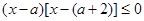 ”的充分不必要条件,则实数
”的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A.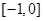 | B.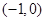 |
C.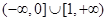 | D.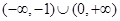 |