题目内容
10. 函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{10π}{3}$)的值为( )
函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{10π}{3}$)的值为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 由函数f(x)的部分图象求出A、B的值,
再根据x=$\frac{2π}{3}$时f(x)取得最大值,x=2π时f(x)=0,
列出方程组求出ω、φ的值,写出f(x)的解析式,再计算f($\frac{10π}{3}$).
解答 解:由函数f(x)=Asin(ωx+φ)+B的部分图象知,
2A=3-(-1)=4,解得A=2,
∴B=$\frac{3-1}{2}$=1;
又x=$\frac{2π}{3}$时,f(x)取得最大值3,
∴$\frac{2π}{3}$ω+φ=$\frac{π}{2}$①;
x=2π时,f(x)=0,
∴2πω+φ=$\frac{7π}{6}$②;
由①②组成方程组,
解得ω=$\frac{1}{2}$,φ=$\frac{π}{6}$;
∴f(x)=2sin($\frac{1}{2}$x+$\frac{π}{6}$)+1,
∴f($\frac{10π}{3}$)=2sin($\frac{1}{2}$×$\frac{10π}{3}$+$\frac{π}{6}$)+1=2×(-$\frac{1}{2}$)+1=0.
故选:B.
点评 本题考查了函数f(x)=Asin(ωx+φ)+B的图象与性质的应用问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知f(x)=$\frac{{e}^{x}}{x}$,若方程f2(x)+2a2=3a|f(x)|有且仅有4个不等实根,则实数a的取值范围为( )
| A. | (0,$\frac{e}{2}$) | B. | ($\frac{e}{2}$,e) | C. | (0,e) | D. | (e,+∞) |
2.集合A={-2,-1,0,1,2},B={-1,2,3},则A∪B=( )
| A. | {-2,-1,0,1,2} | B. | {-1,2,3} | C. | {-2,-1,0,1,2,3} | D. | {-1,2} |
20.已知△ABC的三边长为a,b,c,满足直线ax+by+2c=0与圆x2+y2=4相离,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 钝角三角形 | D. | 以上情况都有可能 |
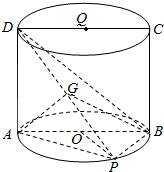 如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.
如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.