题目内容
已知m=∫
dx,则(1-mx)5的展开式中含x3项的系数为 (用具体数字作答).
e2 1 |
| 1 |
| x |
考点:二项式系数的性质,定积分
专题:二项式定理
分析:求定积分得到m=2,在(1-2x)5的展开式的通项公式中令x的幂指数等于3,可得r的值,从而求得(1-2x)5的展开式中含x3项的系数.
解答:
解:m=∫
dx=lnx
=2-0=2,则(1-mx)5=(1-2x)5 ,
故则(1-2x)5的展开式的通项公式为 Tr+1=
•(-2)r•xr,
令r=3,可得(1-2x)5的展开式中含x3项的系数为
•(-2)3=-80,
故答案为:-80.
e2 1 |
| 1 |
| x |
| | | e2 1 |
故则(1-2x)5的展开式的通项公式为 Tr+1=
| C | r 5 |
令r=3,可得(1-2x)5的展开式中含x3项的系数为
| C | 3 5 |
故答案为:-80.
点评:本题主要考查定积分的运算,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题中正确的是( )
| A、若x∈C,则方程x3=2只有一个根 | ||
| B、若z1∈C,z2∈C且z1-z2>0,则z1>z2 | ||
C、若z∈R,则z•
| ||
| D、若z∈C,且z2<0,那么z一定是纯虚数 |
已知函数f(x)=
sin2x+cos2x,且-
≤x≤m+
+
-5(m>1)恒成立,则f(x)的值域为( )
| 3 |
| π |
| 6 |
| 4 |
| m-1 |
| π |
| 2 |
A、[
| ||
B、[1,
| ||
| C、[1,2] | ||
| D、[-1,2] |
程序框图如图所示,若其输出结果是140,则判断框中填写的是( )


| A、i<7 | B、i<8 |
| C、i>7 | D、i>8 |
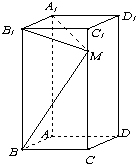 如图所示,在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=4,M为棱CC1上一点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=2,BC=2,CC1=4,M为棱CC1上一点. 如图,函数f(x)=Asin(ωx+φ)(其中
如图,函数f(x)=Asin(ωx+φ)(其中