题目内容
11.如图所示是一个几何体的三视图,则这个几何体的外接球的表面积为32π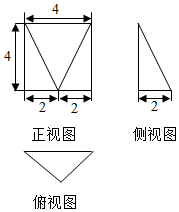
分析 由已知中的三视图可得,该几何体是一个以正视图为底面的四棱锥,其外接球,与以俯视图为底面,以4为高的直三棱柱的外接球相同,进而可得该几何体外接球的表面积
解答 解:由已知中的三视图可得,该几何体是一个以正视图为底面的四棱锥,
其外接球,与以俯视图为底面,以4为高的直三棱柱的外接球相同,
如图所示:
由底面底边长为4,高为2,故底面为等腰直角三角形,
可得底面外接圆的半径为:r=2,
由棱柱高为4,可得球心距为2,
故外接球半径为:R=$\sqrt{{2}^{2}+{2}^{2}}$=2 $\sqrt{2}$,
故外接球的表面积S=4πR2=32π;
故答案为:32π.
点评 本题考查了空间几何体的三视图以及其外接球的表面积求法;关键是正确还原几何体,计算外接球的半径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若不等式ax2+5x-2>0的解集是{x|$\frac{1}{2}$<x<2},则a的值为( )
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -2 | D. | $\frac{1}{2}$ |
19.抛物线y=-$\frac{1}{2}$x2的焦点坐标为( )
| A. | (-$\frac{1}{2}$,0) | B. | (0,-$\frac{1}{4}$) | C. | (0,-$\frac{1}{2}$) | D. | (0,-1) |
20.已知sin2θ=$\frac{3}{7}$,则cos2(θ-$\frac{π}{4}$)的值是( )
| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
1.若命题“?x∈(1,+∞),x2-(2+a)x+2+a≥0”为真命题,则实数a的取值范围是( )
| A. | (-∞,-2] | B. | (-∞,2] | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |