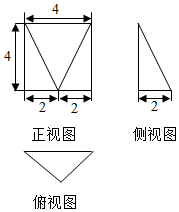
题目内容
20．已知sin2θ=$\frac{3}{7}$，则cos2（θ-$\frac{π}{4}$）的值是（ ）| A． | $\frac{2}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{7}$ |
分析 由条件利用二倍角的余弦公式求得cos2（θ-$\frac{π}{4}$）的值．
解答 解：∵sin2θ=$\frac{3}{7}$，则cos2（θ-$\frac{π}{4}$）=$\frac{1+cos（2θ-\frac{π}{2}）}{2}$=$\frac{1+sin2θ}{2}$=$\frac{5}{7}$，
故选：D．
点评 本题主要考查二倍角的余弦公式的应用，属于基础题．
练习册系列答案
相关题目
15．
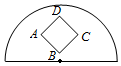如图，在半径为1的半圆内，放置一个边长为$\frac{1}{2}$的正方形ABCD，向半圆内任取一点，则该点落在正方形内的槪率为（ ）
如图，在半径为1的半圆内，放置一个边长为$\frac{1}{2}$的正方形ABCD，向半圆内任取一点，则该点落在正方形内的槪率为（ ）| A． | $\frac{1}{π}$ | B． | $\frac{1}{2π}$ | C． | $\frac{2}{π}$ | D． | $\frac{π}{4}$ |
5．设集合A={x|-3＜x＜4}，集合B={x|x＜log29}，则A∪B等于（ ）
| A． | （-3，log29） | B． | （-3，4） | C． | （-∞，log29） | D． | （-∞，4） |
9．下列结论正确的是（ ）
| A． | 当x＞0且x≠1时，lgx+$\frac{1}{lgx}$≥2 | B． | x＞0时，6-x-$\frac{4}{x}$的最大值是2 | ||
| C． | $\frac{{x}^{2}+5}{\sqrt{{x}^{2}+4}}$的最小值是2 | D． | 当x∈（0，π）时，sinx+$\frac{4}{sinx}$≥4 |