题目内容
已知过点A﹙0,
﹚,B﹙7,0﹚的直线l1与过点C﹙2,1﹚,D﹙3,k+1)的直线l2和两坐标轴围成的四边形内接于一个圆,求实数k的值.
| 7 |
| 3 |
考点:直线的倾斜角
专题:直线与圆
分析:根据四点共圆的条件可知,四边形的2个对角之和是180°,即l1与l2是相互垂直的,利用两条直线斜率的乘积为-1,即可得到结论.
解答:
解:∵过点A﹙0,
﹚,B﹙7,0﹚的直线l1与过点C﹙2,1﹚,D﹙3,k+1)的直线l2和两坐标轴围成的四边形内接于一个圆,
∴根据四点共圆的条件可知l1与l2是相互垂直,
即l1与l2对应的斜率满足k1•k2=-1,
即
•
=-1,
∴-
•
=-1,解得k=3.
| 7 |
| 3 |
∴根据四点共圆的条件可知l1与l2是相互垂直,
即l1与l2对应的斜率满足k1•k2=-1,
即
| ||
| -7 |
| k+1-1 |
| 3-2 |

∴-
| 1 |
| 3 |
| k |
| 1 |
点评:本题主要考查直线垂直与直线斜率之间的关系,利用四点共圆得到直线垂直是解决本题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知a,b,c∈R*,a+b+c=6,M=abc,N=a2+b2+c2,则( )
| A、M<N | B、M>N |
| C、M=N | D、不能确定 |
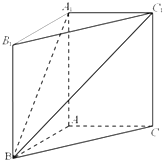 如图,在直三棱柱ABC-A1B1C1中,AC=AB=
如图,在直三棱柱ABC-A1B1C1中,AC=AB=