题目内容
9.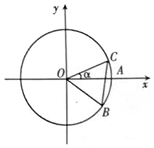 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
分析 根据B的坐标可知圆O是单位圆,可得COB是正三角形,利用三角函数的定义即可求解
解答 解:由B的坐标($\frac{4}{5}$)2+($-\frac{3}{5}$)2=1可知圆O是单位圆,∴△COB是正三角形,
∴$∠BOC=\frac{π}{3}$,$∠AOB=\frac{π}{3}-α$,
由直角三角形中的三角函数的定义可得sin($\frac{π}{3}-α$)=$\frac{3}{5}$,
∴$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$cosα$-\frac{1}{2}$sinα=sin($\frac{π}{3}-α$)=$\frac{3}{5}$
故选B
点评 本题主要考查了单位圆的计算和三角函数的定义的灵活运用能力.属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
20.如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的周长为( )
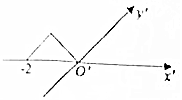

| A. | 2+$\sqrt{2}+\sqrt{6}$ | B. | 4+2$\sqrt{2}$+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+2$\sqrt{3}$ | D. | 4+4$\sqrt{2}$ |
17.已知x>0时,f(x)=x-2013,且知f(x)在定义域上是奇函数,则当x<0时,f(x)的解析式是( )
| A. | f(x)=x+2013 | B. | f(x)=-x+2013 | C. | f(x)=-x-2013 | D. | f(x)=x-2013 |
4.保险柜的密码由0,1,2,3,4,5,6,7,8,9中的四个数字组成,假设一个人记不清自己的保险柜密码,只记得密码全部由奇数组成且按照递增顺序排列,则最多输入2次就能开锁的频率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{5}$ | D. | $\frac{9}{20}$ |
18.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(2,1)在“右”区域内,则双曲线离心率e的取值范围是( )
| A. | $({1,\frac{{\sqrt{5}}}{2}})$ | B. | $({\frac{{\sqrt{5}}}{2},+∞})$ | C. | $({1,\frac{5}{4}})$ | D. | $({\frac{5}{4},+∞})$ |
19.已知i为虚数单位,复数z满足$\overline z(1+i)=i$,则z=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}+\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |