Question

【题目】如图，四棱锥中，底面是平行四边形， , 平面底面，且是边长为的等边三角形， ， 是 中点．

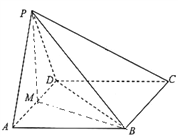
(1)求证：平面平面；

(2)证明： ， 且与的面积相等.

Answer 1

【答案】(1)见解析（2）见解析

【解析】试题分析：（1）由正三角形性质得PM⊥AD，再根据面面垂直性质定理得PM⊥底面ABCD，即得PM⊥BM，利用勾股定理得BM⊥AD，最后根据线面垂直判定定理得BM⊥平面PAD，由面面垂直判定定理得结论（2）利用余弦定理求两角余弦值，结合余弦函数单调性确定两角大小，根据三角形面积公式计算面积，可证相等

试题解析： 解：(1) △PAD是边长为2的等边三角形, M是AD中点

PM⊥AD, PM平面PAD

又平面PAD⊥底面ABCD PM⊥底面ABCD

平面PAD∩底面ABCD=AD

又BM底面ABCD, PM⊥BM, △PMB是直角三角形

在等边△PAD中，PM=，又PB=， MB=

∠BAD=60○, 在△ABM中, 由余弦定理：MB2 = AM2+AB2-2AM×AB×cos60○

得：AB2 - AB -2=0, 即AB=2， △ABD也是等边三角形，

BM⊥AD

平面PAD∩底面ABCD=AD BM⊥平面PAD

BM底面ABCD BM平面PMB 平面PMB⊥平面PAD

（Ⅱ）由（Ⅰ）知底面ABCD是菱形. 连接CM, 在△DMC中，∠MDC=120○,

由余弦定理：MC2 = MD2+CD2-2MD×CD×cos120○ =12+ 22-2×1×2×=7

得： MC=， 在直角形△PMC中， ：PC2 =PM2+MC2=

在△PDC中，由余弦定理：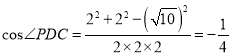

在△PAB中，由余弦定理：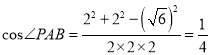

, ，余弦函数在是减函数

∠PDC >∠PAB，

而，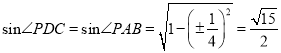

，即△PDC与△PAB面积相等.

(注：没有通过计算出面积，能够说明面积相等原因的，仍然是满分)