题目内容
【题目】已知椭圆![]() :
:![]() 的左、右有顶点分别是
的左、右有顶点分别是![]() 、
、![]() ,上顶点是
,上顶点是![]() ,圆
,圆![]() :
:![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离是
的距离是![]() ,且椭圆的右焦点与抛物线
,且椭圆的右焦点与抛物线![]() 的焦点重合.
的焦点重合.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)平行于![]() 轴的动直线与椭圆和圆在第一象限内的交点分别为
轴的动直线与椭圆和圆在第一象限内的交点分别为![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与
与![]() 轴的交点记为
轴的交点记为![]() ,
,![]() .试判断
.试判断![]() 是否为定值,若是,证明你的结论.若不是,举反例说明.
是否为定值,若是,证明你的结论.若不是,举反例说明.
【答案】(1) ![]() (2)
(2) ![]() 是定值为
是定值为![]()
【解析】试题分析:(Ⅰ)写出![]() 的方程,利用点到直线的距离和抛物线的焦点坐标进行求解;(Ⅱ)设出直线方程,联立直线和椭圆的方程,得到关于
的方程,利用点到直线的距离和抛物线的焦点坐标进行求解;(Ⅱ)设出直线方程,联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用根与系数的关系、点在圆上及平面向量的数量积公式进行求解.
的一元二次方程,利用根与系数的关系、点在圆上及平面向量的数量积公式进行求解.
试题解析:(Ⅰ)![]() 方程为:
方程为:![]() 即为:
即为:![]()
由题意得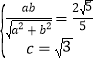
整理得:![]()
![]() ,
,![]() (舍) ∴
(舍) ∴![]()
椭圆![]() :
:![]()
(Ⅱ)设直线![]() :
:![]() ,令
,令![]() 得
得![]() ∴
∴![]()
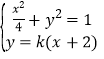
![]()
![]() ∴
∴![]()
∴![]() ∴
∴![]()
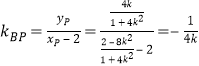
∴![]() 方程为:
方程为:![]()
令![]() 得
得![]() ∴
∴![]()
设![]() ,则
,则![]() 且
且![]()
∴![]()
![]()
![]()
∴![]() 即:
即:![]()
所以![]() 是定值为
是定值为![]()

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目