题目内容
14.P是边长为a的正三角形ABC所在平面外一点,且PA=PB=PC=a,则四面体PABC外接球半径为$\frac{\sqrt{6}}{4}$a.分析 如图所示,AO=$\frac{\sqrt{3}}{3}$a,PO=$\frac{\sqrt{6}}{3}$a,利用勾股定理,即可求出四面体PABC外接球半径.
解答 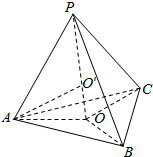 解:如图所示,AO=$\frac{\sqrt{3}}{3}$a,PO=$\frac{\sqrt{6}}{3}$a,
解:如图所示,AO=$\frac{\sqrt{3}}{3}$a,PO=$\frac{\sqrt{6}}{3}$a,
设四面体PABC外接球半径为R,则
R2=($\frac{\sqrt{6}}{3}$a-R)2+($\frac{\sqrt{3}}{3}$a)2,
∴R=$\frac{\sqrt{6}}{4}$a.
故答案为:$\frac{\sqrt{6}}{4}$a.
点评 本题考查四面体PABC外接球半径,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
3.若直线l过点(1,2),在y轴上的截距为1,则l的方程为( )
| A. | 3x-y-1=0 | B. | 3x-y+1=0 | C. | x-y-1=0 | D. | x-y+1=0 |