题目内容
(本小题满分13分)
已知椭圆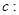
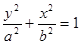 (a>b>0)的离心率
(a>b>0)的离心率
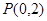 为
为
该椭圆上一点,
(I)求椭圆的方程.
(II)过点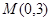 作直线
作直线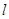 与椭圆
与椭圆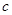 相交于
相交于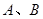 点,若以
点,若以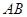 为直径的圆经原点
为直径的圆经原点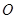 ,求直线
,求直线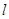 的方程
的方程
已知椭圆
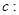
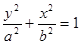 (a>b>0)的离心率
(a>b>0)的离心率
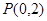 为
为该椭圆上一点,
(I)求椭圆的方程.
(II)过点
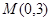 作直线
作直线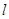 与椭圆
与椭圆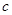 相交于
相交于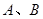 点,若以
点,若以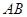 为直径的圆经原点
为直径的圆经原点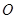 ,求直线
,求直线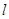 的方程
的方程(I) 椭圆C:
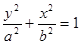 (a>b>0)过点
(a>b>0)过点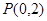 则
则 …………………1分
…………………1分 ,
, …………………………………………………4分
…………………………………………………4分∴椭圆的标准方程是
 ………………………………………………5分
………………………………………………5分(II) 设
 依题设直线
依题设直线 的方程为
的方程为
联立
 得
得 ,
,整理得
 ,…………………………………6分
,…………………………………6分于是
 ,.……………………………7分
,.……………………………7分 ……………………………8分
……………………………8分∴

 ………………………9分
………………………9分由
 知
知 .将(1)式和(2)式代入得
.将(1)式和(2)式代入得 解得
解得
且满足
 …………………………12分
…………………………12分所以所求的直线方程为
 ………………………………………………13分
………………………………………………13分略

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
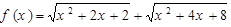 的最小值为( )
的最小值为( )



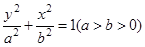 的上焦点是
的上焦点是 ,过点P(3,4)和
,过点P(3,4)和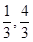 ).
).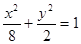 经过点
经过点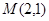 ,
, 为坐标原点,平行于
为坐标原点,平行于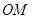 的直线
的直线 在
在 轴上的截距为
轴上的截距为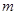
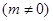 .
.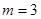 时,判断直线
时,判断直线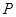 为椭圆上的动点,求点
为椭圆上的动点,求点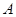 、
、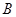 两个不同点时,求证:直线
两个不同点时,求证:直线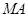 、
、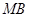 与
与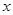 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.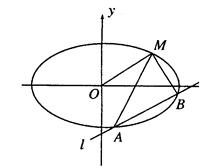
 +
+ =1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )
=1的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为( )


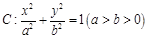 的离心率为
的离心率为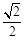 ,其中左焦点
,其中左焦点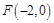
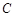 的方程
的方程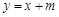 与椭圆
与椭圆 ,且线段
,且线段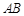 的中
的中 点
点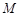 关于直线
关于直线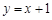 的对称点在圆
的对称点在圆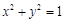 上,求
上,求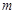 的值
的值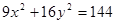 内有一点P
内有一点P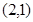 ,以P为中点作弦MN,则直线MN的方程是( )
,以P为中点作弦MN,则直线MN的方程是( )



 的离心率为
的离心率为 ,则
,则 的值为_____________.
的值为_____________.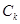 的方程:
的方程: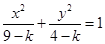 .
.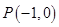 ,是否存在曲线
,是否存在曲线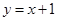 于
于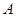 、
、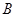 两点,使得
两点,使得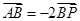 ?若存在,求出
?若存在,求出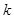 的值;若不存在,说明理由;
的值;若不存在,说明理由;