题目内容
(本题满分18分,第(1)题4分、第(2)题8分、第(3)题6分)
已知二次曲线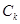 的方程:
的方程: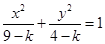 .
.
(1)分别求出方程表示椭圆和双曲线的条件;
(2)对于点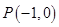 ,是否存在曲线
,是否存在曲线 交直线
交直线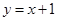 于
于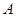 、
、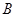 两点,使得
两点,使得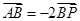 ?若存在,求出
?若存在,求出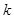 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)已知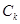 与直线
与直线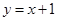 有公共点,求其中实轴最长的双曲线方程.
有公共点,求其中实轴最长的双曲线方程.
已知二次曲线
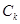 的方程:
的方程: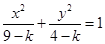 .
.(1)分别求出方程表示椭圆和双曲线的条件;
(2)对于点
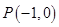 ,是否存在曲线
,是否存在曲线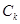 交直线
交直线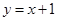 于
于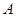 、
、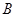 两点,使得
两点,使得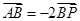 ?若存在,求出
?若存在,求出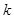 的值;若不存在,说明理由;
的值;若不存在,说明理由;(3)已知
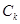 与直线
与直线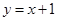 有公共点,求其中实轴最长的双曲线方程.
有公共点,求其中实轴最长的双曲线方程.
略

练习册系列答案
相关题目
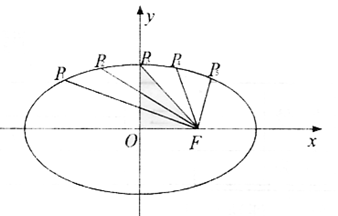
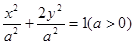 ,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上
,其右焦点为F,把椭圆的长轴分成6等分,过每个等分点作x轴的垂线交椭圆上 半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5
半部于点P1,P2,P3,P4,P5五个点,且|P1F|+|P2F|+|P3F|+|P4F|+|P5F|=5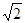 .
.
 x与椭圆C:
x与椭圆C: =1(a>b>0)交于A、B两点,以线段AB为直径的圆恰好经过椭圆的右焦点,则椭圆C的离心率为.
=1(a>b>0)交于A、B两点,以线段AB为直径的圆恰好经过椭圆的右焦点,则椭圆C的离心率为. B.
B. C.
C. D.4-2
D.4-2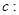
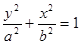 (a>b>0)的离心率
(a>b>0)的离心率
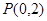 为
为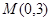 作直线
作直线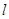 与椭圆
与椭圆 相交于
相交于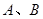 点,若以
点,若以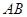 为直径的圆经原点
为直径的圆经原点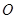 ,求直线
,求直线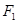 、
、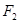 分别是椭圆
分别是椭圆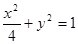 的左、右焦点.
的左、右焦点.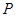 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求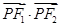 的最大值和最小值;
的最大值和最小值;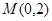 的直线
的直线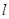 与椭圆交于不同的两点
与椭圆交于不同的两点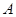 、
、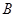 ,且∠
,且∠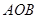 为锐角(其中
为锐角(其中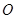 为坐标原点),求直线
为坐标原点),求直线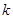 的取值范围.
的取值范围.
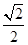


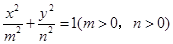 的右焦点为
的右焦点为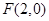 ,离心率为
,离心率为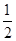 ,则此椭圆的方程为___________
,则此椭圆的方程为___________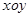 中,向量
中,向量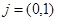 ,△OFP的面积为
,△OFP的面积为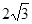 ,且
,且
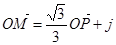 。
。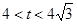 ,求向量
,求向量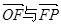 的夹角
的夹角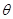 的取值范围;
的取值范围;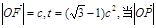 取最小值时,求椭圆的方程。
取最小值时,求椭圆的方程。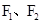 分别是椭圆
分别是椭圆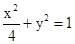 的左右焦点,若P是该椭圆上的一个动点则
的左右焦点,若P是该椭圆上的一个动点则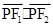 最大值和最小值分别是 ( )
最大值和最小值分别是 ( )


