��Ŀ����
��֪����f��x��=
x2-��a-1��x+alnx�������a��R��
����a=6ʱ������f��x���ļ�ֵ�㣻
����֤����������x��[1��+�ޣ���lnx��
�������
�����ں���f��x��ͼ���ϵIJ�ͬ����A��x1��y1����B��x2��y2����x1��x2��������ں���f��x��ͼ���ϴ��ڵ�M��x0��y0��������x0�ʣ�x1��x2������ʹ���ڵ�M��������l��AB�����ֱ��AB���ڡ��������ߡ����ر�أ���x0=
���ֳ�ֱ��AB���ڡ���ֵ�������ߡ������ʣ���a=1ʱ�����ں���f��x��ͼ���ϲ�ͬ����A��B��ֱ��AB�Ƿ���ڡ���ֵ�������ߡ�����֤����Ľ��ۣ�
| 1 |
| 2 |
����a=6ʱ������f��x���ļ�ֵ�㣻
����֤����������x��[1��+�ޣ���lnx��
| 2(x-1) |
| x+1 |
�����ں���f��x��ͼ���ϵIJ�ͬ����A��x1��y1����B��x2��y2����x1��x2��������ں���f��x��ͼ���ϴ��ڵ�M��x0��y0��������x0�ʣ�x1��x2������ʹ���ڵ�M��������l��AB�����ֱ��AB���ڡ��������ߡ����ر�أ���x0=
| x1+x2 |
| 2 |
���㣺�������������,���õ����о������ĵ�����,���õ����о������ļ�ֵ
ר�⣺�������ۺ�Ӧ��
����������a=6ʱ���������������ݺ�����ֵ�͵���֮��Ĺ�ϵ��������f��x���ļ�ֵ�㣻
�����캯��g��x��=lnx-
�������ĵ���������֤������ʽ��
�����ݡ���ֵ�������ߡ��Ķ��壬�������ƽ�к�б��֮��Ĺ�ϵ�����ɵõ����ۣ�
�����캯��g��x��=lnx-
| 2(x-1) |
| x+1 |
�����ݡ���ֵ�������ߡ��Ķ��壬�������ƽ�к�б��֮��Ĺ�ϵ�����ɵõ����ۣ�
���
�⣺����a=6ʱ��f��x��=
x2-5x+6lnx��
f�䣨x��=x-5+
=
����x��0����
��f�䣨x��=0ʱ�����x=2��x=3��
��0��x��2��x��3ʱ��f�䣨x����0����f��x���ڣ�0��2������3��+�ޣ��ϵ���������
��2��x��3ʱ��f�䣨x����0��f��x���ڣ�2��3���ϵ����ݼ���
��x=2Ϊ����f��x���ļ���ֵ�㣬x=3Ϊ����f��x���ļ�Сֵ�㣮
������g��x��=lnx-
����x��1����
��g�䣨x��=
-
=
��
��x��1����g�䣨x����0��
��g��x����[1��+�ޣ��ϵ�����
��g��x����g��1��=0�����ҽ���x=1ʱ�Ⱥų�������
��֤��������x��[1��+�ޣ���lnx��
�������
�� III����a=1��f��x��=
x2-+lnx��x��0��
f�䣨x��=x+
�����躯��f��x�����ڡ���ֵ�������ߡ���
��A��x1��y1����B��x2��y2����x1��x2����M��x0��y0��������y=f��x���ϵIJ�ͬ�㣬��0��x1��x2��x0=
��
��ֱ��AB��б�ʣ�kAB=
=
=
��x1+x2��+
��
�����ڵ�M��x0��y0����������б�ʣ�k=f�䣨x0��=f�䣨
��=
+
��
�����⣺kAB=k����
��x1+x2��+
=
+
��
�����
=
��
��ln
=
=
��
��t=
����t��1����ʽ��Ϊlnt=
��
�ɣ�2��֪t��1ʱ��lnx��
�������
���ڣ�1��+�ޣ��ڲ�����t��ʹ��lnt=
������
�������������費���������ԣ�����f��x�������ڡ���ֵ�������ߡ���
| 1 |
| 2 |
f�䣨x��=x-5+
| 6 |
| x |
| x2-5x+6 |
| x |
��f�䣨x��=0ʱ�����x=2��x=3��
��0��x��2��x��3ʱ��f�䣨x����0����f��x���ڣ�0��2������3��+�ޣ��ϵ���������
��2��x��3ʱ��f�䣨x����0��f��x���ڣ�2��3���ϵ����ݼ���
��x=2Ϊ����f��x���ļ���ֵ�㣬x=3Ϊ����f��x���ļ�Сֵ�㣮
������g��x��=lnx-
| 2(x-1) |
| x+1 |
��g�䣨x��=
| 1 |
| x |
| 2(x+1)-2(x-1) |
| (x+1)2 |
| (x-1)2 |
| x(x+1)2 |
��x��1����g�䣨x����0��
��g��x����[1��+�ޣ��ϵ�����
��g��x����g��1��=0�����ҽ���x=1ʱ�Ⱥų�������
��֤��������x��[1��+�ޣ���lnx��
| 2(x-1) |
| x+1 |
�� III����a=1��f��x��=
| 1 |
| 2 |
f�䣨x��=x+
| 1 |
| x |
��A��x1��y1����B��x2��y2����x1��x2����M��x0��y0��������y=f��x���ϵIJ�ͬ�㣬��0��x1��x2��x0=
| x1+x2 |
| 2 |
��ֱ��AB��б�ʣ�kAB=
| y2-y1 |
| x2-x1 |
| ||||
| x2-x1 |
| 1 |
| 2 |
| lnx2-lnx1 |
| x2-x1 |
�����ڵ�M��x0��y0����������б�ʣ�k=f�䣨x0��=f�䣨
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
�����⣺kAB=k����
| 1 |
| 2 |
| lnx2-lnx1 |
| x2-x1 |
| x1+x2 |
| 2 |
| 2 |
| x1+x2 |
�����
| lnx2-lnx1 |
| x2-x1 |
| 2 |
| x1+x2 |
��ln
| x2 |
| x1 |
| 2(x2-x1) |
| x1+x2 |
2(
| ||
|
��t=
| x2 |
| x1 |
| 2(t-1) |
| t+1 |
�ɣ�2��֪t��1ʱ��lnx��
| 2(x-1) |
| x+1 |
���ڣ�1��+�ޣ��ڲ�����t��ʹ��lnt=
| 2(t-1) |
| t+1 |
�������������費���������ԣ�����f��x�������ڡ���ֵ�������ߡ���
������������Ҫ���麯���ļ�ֵ�͵����Ĺ�ϵ���ۺϿ��鵼����Ӧ�ã�����ѧ���������������ۺ��Խ�ǿ���������ϴ�

��ϰ��ϵ�д�
�����Ŀ
һ�����������У����������棬�������ٵ�һ�����У������������㣬�������ٵ�һ����̨�У������������⣮
| A��8 4 6 |
| B��5 4 3 |
| C��4 4 4 |
| D��4 6 3 |
��֪ʵ��x��y����
����z=
��ȡֵ��ΧΪ��������
|
| 2x+y+2 |
| x |
A��[0��
| ||
B����-�ޣ�0]��[
| ||
C��[2��
| ||
D����-�ޣ�2]��[
|
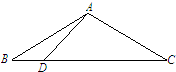 ��ͼ����ABC�У�AB=AC=2��BC=2
��ͼ����ABC�У�AB=AC=2��BC=2