题目内容
15.函数y=$\frac{1}{|1-x|}$的图象与函数y=2cosπx(-2≤x≤4)的图象所有交点的横坐标之和等于( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 在同一个坐标系中画出函数y=$\frac{1}{|1-x|}$=$\frac{1}{|x-1|}$ 的图象以及函数y=2cosπx的图象,根据题意可得它们的交点也关于直线x=1对称,从而求得所有交点的横坐标之和.
解答 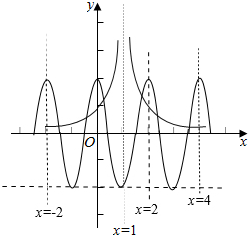 解:∵函数y=$\frac{1}{|1-x|}$=$\frac{1}{|x-1|}$ 的图象(图中蓝色部分)
解:∵函数y=$\frac{1}{|1-x|}$=$\frac{1}{|x-1|}$ 的图象(图中蓝色部分)
关于直线x=1对称,
函数y=2cosπx的图象(图中黑色部分)也关于
直线x=1对称,
故它们的交点也关于直线x=1对称,如图所示,
故在[-2,4]上,它们的图象所有交点共有6个,
且这6个交点关于直线x=1对称,
故这6个交点的横坐标之和为2+2+2=6,
故选:C.
点评 本题主要考查函数的图象的对称性,属于中档题.

练习册系列答案
相关题目
5.若sinα-sinβ=1-$\frac{\sqrt{3}}{2}$,cosα-cosβ=-$\frac{1}{2}$,则cos(α-β)的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | 1 |
8.下列函数,既是奇函数又在区间(0,+∞)上单调递增的函数是( )
| A. | y=$\frac{1}{x}$ | B. | y=2|x| | C. | y=-log${\;}_{\frac{1}{2}}$x | D. | y=x|x| |
9.计算:lg2+lg5=( )
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
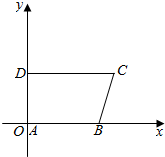 设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.
设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.