题目内容
1.已知a>0,b>0,且$\frac{1}{a}+\frac{2}{b}$=2.(1)求ab的最小值;
(2)求a+2b的最小值,并求出a、b相应的取值.
分析 (1)运用基本不等式m+n≥2$\sqrt{mn}$(m,n>0),当且仅当m=n取得等号,计算即可得到最小值;
(2)运用乘1法和基本不等式即可得到最小值,注意等号成立的条件.
解答 解:(1)由a>0,b>0,且$\frac{1}{a}+\frac{2}{b}$=2,
可得2=$\frac{1}{a}$+$\frac{2}{b}$≥2$\sqrt{\frac{2}{ab}}$,
即ab≥2,当且仅当b=2a=2时取得等号,
则ab的最小值为2;
(2)a+2b=$\frac{1}{2}$(a+2b)($\frac{1}{a}$+$\frac{2}{b}$)=$\frac{1}{2}$(5+$\frac{2b}{a}$+$\frac{2a}{b}$)≥$\frac{1}{2}$(5+2$\sqrt{\frac{2b}{a}•\frac{2a}{b}}$)=$\frac{9}{2}$;
等号成立的充要条件是a=b=$\frac{3}{2}$,
∴a+2b的最小值为$\frac{9}{2}$;此时a=b=$\frac{3}{2}$.
点评 本题考查基本不等式的运用:求最值,注意满足的条件:一正二定三等,同时注意运用乘1法,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
10.已知直线l:x+y-4=0,定点P(2,0),E,F分别是直线l和y轴上的动点,则△PEF的周长的最小值为( )
| A. | 2$\sqrt{10}$ | B. | 6 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{5}$ |
11.“2<m<6”是“方程(6-m)x2+(m-2)y2=-m2+8m-12表示椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
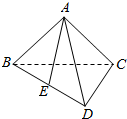 如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.
如图,在三棱锥A-BCD中,侧面ABC是一个等腰直角三角形,∠BAC=90°,底面BCD是一个等边三角形,平面ABC⊥平面BCD,E为BD的中点,则AE与平面BCD所成角的大小为45°.