题目内容
19.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),点A、F分别为其右顶点和右焦点,B1(0,b),B2(0,-b),若B1F⊥B2A,则该双曲线的离心率为( )| A. | $1+\sqrt{5}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}-1$ |
分析 根据题意,设A(a,0),F(c,0),由向量的坐标计算公式可得$\overrightarrow{{B}_{1}F}$=(c,-b),$\overrightarrow{{B}_{2}A}$=(a,b),进而分析可得$\overrightarrow{{B}_{1}F}$•$\overrightarrow{{B}_{2}A}$=ac-b2=0,结合双曲线的几何性质,可得c2-a2-ac=0,由离心率公式变形可得e2-e-1=0,解可得e的值,即可得答案.
解答 解:根据题意,已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),点A、F分别为其右顶点和右焦点,
设A(a,0),F(c,0),
则$\overrightarrow{{B}_{1}F}$=(c,-b),$\overrightarrow{{B}_{2}A}$=(a,b),
若B1F⊥B2A,则有$\overrightarrow{{B}_{1}F}$•$\overrightarrow{{B}_{2}A}$=ac-b2=0,
又由c2=a2+b2,
则有c2-a2-ac=0,
变形可得:e2-e-1=0,
解可得e=$\frac{1+\sqrt{5}}{2}$或$\frac{1-\sqrt{5}}{2}$(舍)
故e=$\frac{1+\sqrt{5}}{2}$,
故选:C.
点评 本题考查双曲线的几何性质,关键是由B1F⊥B2A分析a、b、c的关系.

练习册系列答案
相关题目
8.方程ex=2-x的根位于( )
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
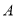 如果满足:①
如果满足:① ;②若对
;②若对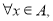 有
有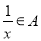 ,则称
,则称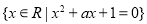 ;
;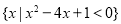 ;
; .其中“互倒集”的个数是( )
.其中“互倒集”的个数是( )