题目内容
14.已知函数f(x)=$\frac{2x}{{x}^{2}+6}$.(1)若f(x)>k的解集为{x|x<-3或x>-2},则k的值等于-$\frac{2}{5}$;
(2)对任意x>0,f(x)≤t恒成立,则t的取值范围是[$\frac{\sqrt{6}}{6}$,+∞).
分析 (1)根据不等式和方程之间的关系,转化为方程进行求解即可.
(2)任意x>0,f(x)≤t恒成立,等等价于t≥$\frac{2x}{{x}^{2}+6}$=$\frac{2}{x+\frac{6}{x}}$恒成立,根据基本不等式即可求出.
解答 解:(1):f(x)>k?kx2-2x+6k<0.
由已知{x|x<-3,或x>-2}是其解集,
得kx2-2x+6k=0的两根是-3,-2.
由根与系数的关系可知(-2)+(-3)=$\frac{2}{k}$,
解得k=-$\frac{2}{5}$,
(2)任意x>0,f(x)≤t恒成立,等价于t≥$\frac{2x}{{x}^{2}+6}$=$\frac{2}{x+\frac{6}{x}}$恒成立,
∵x+$\frac{6}{x}$≥2$\sqrt{x•\frac{6}{x}}$=2$\sqrt{6}$,当且仅当x=$\sqrt{6}$时取等号,
∴t≥$\frac{\sqrt{6}}{6}$,
故答案为:(1):-$\frac{2}{5}$,(2):[$\frac{\sqrt{6}}{6}$,+∞)
点评 本题主要考查不等式的应用以及不等式恒成立的问题,根据不等式的解集和方程的根之间的关系是解决本题的关键,属于中档题

练习册系列答案
相关题目
4.函数f(x)=log0.5(x2-4)的单调递增区间是( )
| A. | (-∞,0) | B. | (-∞,-2) | C. | (0,+∞) | D. | (2,+∞) |
19.已知AB是经过抛物线y2=2px的焦点的弦,若点A、B的横坐标分别为1和$\frac{1}{4}$,则该抛物线的准线方程为( )
| A. | x=1 | B. | x=-1 | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
6.在复平面内,复数z=-2+i对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
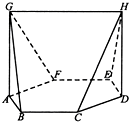 如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且
如图,在七面体ABCDEFGH中,底面ABCDEF是边长为2的正六边形,AG=DH=3,且