题目内容
在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2,E,F,G,分别是线段PC,PD,DA的中点,现将△PDC折起,使平面PDC⊥平面ABCD
(1)求证:平面PAB∥平面EFG.
(2)求证:AD⊥PC.
(3)求二面角G-EF-D的平面角的大小.
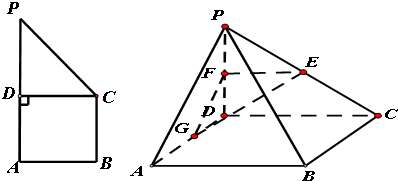
(1)求证:平面PAB∥平面EFG.
(2)求证:AD⊥PC.
(3)求二面角G-EF-D的平面角的大小.

考点:二面角的平面角及求法,平面与平面平行的判定,直线与平面垂直的性质
专题:综合题,空间位置关系与距离,空间角
分析:(1)证明EF∥平面PAB,即证EF∥AB,同理FG∥平面PAB,根据平面与平面平行的判定定理可得;
(2)证明AD⊥PC,只需证明AD⊥面PDC即可;
(3)判断∠DFG为所求即可.
(2)证明AD⊥PC,只需证明AD⊥面PDC即可;
(3)判断∠DFG为所求即可.
解答:
(1)证明:∵E,F分别是PC,PD的中点,
∴ED∥CD,
∵AB∥CD,
∴EF∥AB,
∴EG∥平面PAB
∵EF?平面PAB,AB⊆平面PAB
∴EF∥平面PAB;
同理FG∥平面PAB
又∵FG,EF?平面EFG,FG∩EF=F
∴平面PAB∥平面EFG;
(2)证明:由已知可得CD⊥AP,AD⊥DC,面PDC⊥面ABCD,DC为交线
∴PD⊥面ABCD
∴PD⊥AD,
又∵PD∩DC=D
∴AD⊥面PDC,
∴AD⊥PC;
(3)解:由(2)可知PD⊥EF,GF⊥EF
∴∠DFG为所求
又∵DF=DG=1,PD⊥DG
∴∠DFG=45°.
∴ED∥CD,
∵AB∥CD,
∴EF∥AB,
∴EG∥平面PAB
∵EF?平面PAB,AB⊆平面PAB
∴EF∥平面PAB;
同理FG∥平面PAB
又∵FG,EF?平面EFG,FG∩EF=F
∴平面PAB∥平面EFG;
(2)证明:由已知可得CD⊥AP,AD⊥DC,面PDC⊥面ABCD,DC为交线
∴PD⊥面ABCD
∴PD⊥AD,
又∵PD∩DC=D
∴AD⊥面PDC,
∴AD⊥PC;
(3)解:由(2)可知PD⊥EF,GF⊥EF
∴∠DFG为所求
又∵DF=DG=1,PD⊥DG
∴∠DFG=45°.
点评:本题主要考查面面平行的判定定理的应用,考查线面垂直的判定定理的应用,考查面面角,难度中等.

练习册系列答案
相关题目
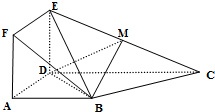 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD丄CD,AB∥CD,AB=AD=
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD丄CD,AB∥CD,AB=AD=