题目内容

3．已知直线l1：y=kx，l2：y=2x+3，若两直线垂直，则k=-$\frac{1}{2}$．

分析 根据直线的垂直关系求出k的值即可．

解答 解：直线l1：y=kx，l2：y=2x+3，
若两直线垂直，则2k=-1，解得：k=-$\frac{1}{2}$，
故答案为：-$\frac{1}{2}$．

点评 本题考查了直线的垂直关系，掌握k1•k2=-1是解题的关键．

练习册系列答案
相关题目
13．已知f（x）的图象与g（x）=（$\frac{1}{2}$）x的图象关于直线y=x对称，那么f（2x-x2）的值域是（　　）
A．RB．（-∞，0]C．（0，+∞）D．[0，+∞）
14．在△ABC中，BC=8，BC边上的高为6，则$\overrightarrow{AB}$•$\overrightarrow{AC}$的取值范围为[20，+∞）．
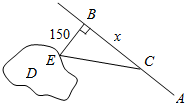11．如图，一海岛D，海岛离岸边最近点B的距离是150km，在岸边距点B300km的点A处有一批物资需运往海岛D，为了尽快送达海岛，A与B之间有一铁路，现用海陆联运的方式，火车的时速为50km，船的时速为30km，试在岸边选一点C，问选在何处可使运输时间最短．
18．已知sina=$\frac{4\sqrt{3}}{7}$，cos（α+β）=-$\frac{11}{14}$，0＜α＜$\frac{π}{2}$，0＜β＜$\frac{π}{2}$．求cosβ
8．函数y=x4+2x2-1的值域[-1，+∞）；函数y=$\frac{1}{{x}^{2}+1}$的值域（0，1]．
3．如图给出的是计算$1+\frac{1}{3}+\frac{1}{5}+…+\frac{1}{2011}$的值的一个程序框图，其中判断框内应填入的条件是（　　）
A．i≤2011B．i＞2011C．i≤1005D．i＞1005
20．若直线l1：mx+y-1=0与直线l2：x+（m-1）y+2=0垂直，则实数m=$\frac{1}{2}$．
1．已知函数g（x）=ax2-2ax+1+b（a＞0）在区间[2，3]上有最小值1和最大值4，设f（x）=$\frac{g（x）}{x}$．
（1）求a，b的值；
（2）若不等式f（x）-kx≥0在区间[$\frac{1}{2}$，2]上有解．求实数k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网