题目内容
已知椭圆E的长轴的一个端点是抛物线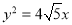
的焦点，离心率是
．
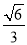（1）求椭圆E的方程；
（2）过点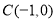
，斜率为k的动直线与椭圆E相交于A、B两点，请问x轴上是否存在点M，使
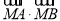为常数？若存在，求出点M的坐标；若不存在，请说明理由．
（1）
；（2）存在点
满足题意．
【解析】
试题分析：（1）根据题意椭圆的焦点在
轴上，抛物线的焦点为
，所以椭圆的一个焦点为
，离心率为
，联立解得椭圆的方程；（2）设直线方程为
代入椭圆方程中，由韦达定理解得
，同时设
进而求得的
解析式满足定值的条件，找到
，得到
点的坐标．
试题解析：（1）根据条件可知椭圆的焦点在x轴，
且
故所求方程为
即
．
（2）假设存在点M符合题意，设AB：
代入
得：
,则
要使上式与K无关，则有
，解得
，存在点
满足题意．
考点：1．椭圆的标准方程；2．韦达定理；3．定点问题．
练习册系列答案
相关题目
．
，第三年比第二年增长
，又这两年的平均增长率为
，则
与
的关系为（ ）．
B、
C、
D、
中，已知
，则B= ．
，集合
，则
（ ）
B、
C、
D、
已知函数
的定义域为
，部分对应值如下表：
| | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
的导函数
的图象如图所示，
下列关于
的命题：
①函数
是周期函数；
②函数
在
上是减函数；
③如果当
时，
的最大值是2，那么
的最大值是4；
④当
时，函数
有4个零点；
⑤函数
的零点个数可能为0，1，2，3，4．其中正确命题的序号是_____________（写出所有正确命题的序号）．
，其图象在点
处的切线
与直线
垂直，则直线
与坐标轴围成的三角形的面积为（ ）
B．
C．
D．
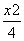＋y2＝1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．
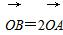，求直线AB的方程．