题目内容
设f(x)(x∈R)为偶函数,且f(x-
)=f(x+
)恒成立,当x∈[2,3]时,f(x)=x,则当x∈[-2,0]时,f(x)= .
| 3 |
| 2 |
| 1 |
| 2 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据条件求出函数的周期是2,利用函数的周期和奇偶性即可求出f(x)在[-2,0]上的表达式.
解答:
解:∵f(x-
)=f(x+
),
∴f(x)=f(x+2),
即函数f(x)的周期是2.
当x∈[0,1]时,x+2∈[2,3],
∴f(x)=f(x+2)=x+2,x∈[0,1],
∵函数f(x)是偶函数,
∴当x∈[-1,0]时,f(x)=f(-x)=-x+2,
当x∈[-2,-1]时,x+2∈[0,1],
此时f(x)=f(x+2)=x+2+2=x+4,
∴当x∈[-2,0]时,f(x)=
,
故答案为:f(x)=
.
| 3 |
| 2 |
| 1 |
| 2 |
∴f(x)=f(x+2),
即函数f(x)的周期是2.
当x∈[0,1]时,x+2∈[2,3],
∴f(x)=f(x+2)=x+2,x∈[0,1],
∵函数f(x)是偶函数,
∴当x∈[-1,0]时,f(x)=f(-x)=-x+2,
当x∈[-2,-1]时,x+2∈[0,1],
此时f(x)=f(x+2)=x+2+2=x+4,
∴当x∈[-2,0]时,f(x)=
|
故答案为:f(x)=
|
点评:本题主要考查函数表达式的求法,利用条件求出函数的周期,利用函数的周期性和奇偶性是解决本题的关键.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,若S10=15,则a3+a8=( )
| A、3 | B、6 | C、9 | D、12 |
在数列1,3,6,10,15,x,28中,x的值为( )
| A、17 | B、20 |
| C、21 | D、以上都可以 |
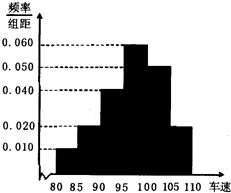 2014年春节期间,高速公路车辆剧增.高管局侧控中心在一特定位置从七座以下小型汽车中按先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆进行电子测速调查,将它们的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105).[105,110)后得到如图所示的频率分布直图.
2014年春节期间,高速公路车辆剧增.高管局侧控中心在一特定位置从七座以下小型汽车中按先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆进行电子测速调查,将它们的车速(km/h)分成六段[80,85),[85,90),[90,95),[95,100),[100,105).[105,110)后得到如图所示的频率分布直图.