题目内容
1.已知二项式(x5-$\frac{1}{x}$)n的展开式中含有非零常数项,则正整数n的最小值为6.分析 利用二项式展开式的通项公式中x项的指数等于0,求出n与r的关系,再结合n为正整数,即可得出答案.
解答 解:由二项式系数的性质,可得其展开式的通项公式为
Tr+1=Cnr(x5)n-r(-$\frac{1}{x}$)r=Cnr(-1)r(x)5n-6r,
根据题意,其展开式中有非零常数项,则有5n-6r=0,
解得r=$\frac{5n}{6}$,即5n为6的整数倍,且n为正整数;
所以n的最小值为6.
故答案为:6.
点评 本题考查了二项式系数的性质与应用问题,解题的关键是牢记二项式的通项公式.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
16.由不等式$\left\{\begin{array}{l}0≤x≤1\\ 0≤y≤1\end{array}\right.$确定的平面区域记为Ω1,不等式$\left\{\begin{array}{l}{(x-\frac{1}{2})^2}+{(y-\frac{1}{2})^2}≤\frac{1}{2}\;\;\\ x≥y\\ x+y≥1\\ \;\;\end{array}\right.$确定的平面区域记为Ω2,在Ω1中随机取一点,则该点恰好在Ω2内的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
6.函数y=x2cosx的部分图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
13.若复数z满足z(2-i)=10+5i(i为虚数单位),则|z|=( )
| A. | 25 | B. | 10 | C. | 5 | D. | $\sqrt{5}$ |
11.函数y=sin($\frac{π}{3}$-$\frac{1}{2}$x),x∈[-2π,2π]的单调递增区间是( )
| A. | [-$\frac{π}{3}$,$\frac{5π}{3}$] | B. | [-2π,-$\frac{π}{3}$] | C. | [$\frac{5π}{3}$,2π] | D. | [-2π,-$\frac{π}{3}$]和[$\frac{5π}{3}$,2π] |
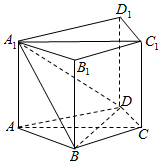 如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.
如图,在直四棱柱ABCD-A1B1C1D1中,∠BAD=60°,AB=BD,BC=CD.