题目内容
12.设等差数列{an}的前n项和为Sn,且满足S2015>0,S2016<0,若对任意正整数n,都有|an|≥|ak|,则k的值为( )| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
分析 等差数列{an}的前n项和为Sn,且满足S2015>0,S2016<0,利用求和公式可得:$\frac{2015({a}_{1}+{a}_{2015})}{2}$=2015a1008>0,$\frac{2016({a}_{1}+{a}_{2016})}{2}$=1008(a1008+a1009)<0,可得a1008>0,a1009<0,即可得出.
解答 解:∵等差数列{an}的前n项和为Sn,且满足S2015>0,S2016<0,
∴$\frac{2015({a}_{1}+{a}_{2015})}{2}$=2015a1008>0,$\frac{2016({a}_{1}+{a}_{2016})}{2}$=1008(a1008+a1009)<0,
∴a1008>0,a1009<0,
∵对任意正整数n,都有|an|≥|ak|,
则k=1008.
故选:C.
点评 本题考查了等差数列的通项公式与求和公式及其性质、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
9.函数y=x2+bx+c在[0,+∞)上是单调函数的充分条件是( )
| A. | b>1 | B. | b<-1 | C. | b<0 | D. | b>-1 |
1.若a1、b1、c1、a2、b2、c2∈R,且都不为零,则“$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$”是“关于x的不等式a1x2+b1x+c1>0与a2x2+b2x+c2>0的解集相同”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
 在长方体ABCD-A1B1C1D1中,AA1=AD=4,E是棱CD上的一点.
在长方体ABCD-A1B1C1D1中,AA1=AD=4,E是棱CD上的一点.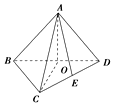 在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.
在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为90°.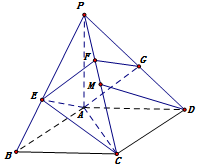 如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.
如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.