题目内容
19.设向量$\overrightarrow{OA}$=(1,-2),$\overrightarrow{OB}$=(a,-1),$\overrightarrow{OC}$=(-b,0),其中 O 为坐标原点,a>0,b>0,若 A,B,C 三点共线,则$\frac{1}{a}$+$\frac{2}{b}$的最小值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
分析 利用向量共线定理可得:2a+b=1.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:$\overrightarrow{AB}$=(a-1,1),$\overrightarrow{AC}$=(-b-1,2),
∵A,B,C 三点共线,∴2(a-1)-(-b-1)=0,化为:2a+b=1.
又a>0,b>0,则$\frac{1}{a}$+$\frac{2}{b}$=(2a+b)$(\frac{1}{a}+\frac{2}{b})$=4+$\frac{b}{a}$+$\frac{4a}{b}$≥4+2$\sqrt{\frac{b}{a}×\frac{4a}{b}}$=8,当且仅当b=2a=$\frac{1}{2}$时取等号.
故选:C.
点评 本题考查了向量共线定理、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.命题“ax2-2ax+3>0恒成立”是假命题,则实数a的取值范围是( )
| A. | 0<a<3 | B. | a<0或a≥3 | C. | a<0或a>3 | D. | a≤0或a≥3 |
11.设命题$p:?x∈R,{x^2}-x+\frac{1}{4}≥0$,则¬p为( )
| A. | $?x∈R,x_{\;}^2-x+\frac{1}{4}≥0$ | B. | $?x∈R,x_{\;}^2-x+\frac{1}{4}<0$ | ||
| C. | $?x∈R,x_{\;}^2-x+\frac{1}{4}≤0$ | D. | $?x∈R,{x^2}-x+\frac{1}{4}<0$ |
11.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 16π | B. | 8π | C. | $\frac{16}{3}$π | D. | $\frac{8}{3}$π |
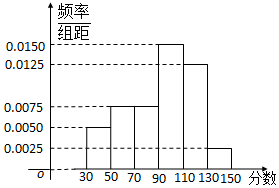 从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图:
从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图: 中,
中,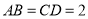 ,
,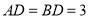 ,
,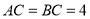 ,点
,点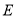 ,
, ,
, ,
,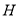 分别在棱
分别在棱 ,
, ,
,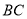 ,
, 上,若直线
上,若直线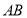 ,
,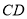 都平行于平面
都平行于平面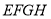 ,则四边形
,则四边形 面积的最大值是( )
面积的最大值是( )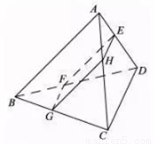
 B.
B.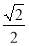 C.
C. D.
D.