题目内容
已知集合A={x|3≤x＜6}，B={y|y=2x，2≤x＜3}：分别求：
（1）A∩B；
（2）∁RB∪A．
（1）A∩B；
（2）∁RB∪A．
考点：交、并、补集的混合运算
专题：集合
分析：由指数函数的性质求出集合B，由补集的运算求出∁RB，
（1）由题意和交集的运算求出A∩B；
（2）由并集的运算求出∁RB∪A．
（1）由题意和交集的运算求出A∩B；
（2）由并集的运算求出∁RB∪A．
解答：
解：由2≤x＜3的，4≤2x＜8，则集合B=[4，8），
所以∁RB=（-∞，4）∪[8，+∞），
（1）集合A={x|3≤x＜6}=[4，6），
所以A∩B=[4，6）；
（2）集合A={x|3≤x＜6}=[4，6），
所以∁RB∪A=（-∞，6）∪[8，+∞）．
所以∁RB=（-∞，4）∪[8，+∞），
（1）集合A={x|3≤x＜6}=[4，6），
所以A∩B=[4，6）；
（2）集合A={x|3≤x＜6}=[4，6），
所以∁RB∪A=（-∞，6）∪[8，+∞）．
点评：本题考查了交、并、补集的混合运算，属于基础题．
练习册系列答案
相关题目
设全集R，A={x|x＞0}，B={x|x＞1}，则A∩∁RB=（ ）
| A、{x|0≤x＜1} |
| B、{x|0＜x≤1} |
| C、{x|x＜0} |
| D、{x|x＞1} |
已知点M(2，
)在幂函数f（x）的图象上，则f（x）的表达式为（ ）
| ||
| 2 |
A、f（x）=x
| ||
B、f（x）=x -
| ||
| C、f（x）=x2 | ||
| D、f（x）=x-2 |
下列两集合表示同一集合的是（ ）
| A、M={1，2}，N={（1，2）} |
| B、M={y=lgx2}，N={y=2lgx} |
| C、M={x|x+y=1}，N={y|x+y=1} |
| D、M={y|y=x2}，N={y|y=2x} |
集合{（x，y）|xy≥0，x∈R，y∈R}是指（ ）
| A、第一象限内的所有点 |
| B、第三象限内的所有点 |
| C、第一象限和第三象限内的所有点 |
| D、不在第二象限、第四象限内的所有点 |
某几何体的三视图如图所示，根据图中标出的数据，可得这个几何体的体积为（ ）
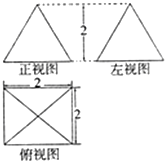
A、4+4
| ||
B、4+4
| ||
C、
| ||
| D、12 |