题目内容

8．已知集合A={x|x2-x-6≤0}，B={x|x＞1}，则A∩B=（　　）
A．[-2，3]B．（1，3]C．（1，3）D．（1，2]

分析 先解出集合A，由（x+2）（x-3）≤0得出A={x|-2≤x≤3}，再确定A∩B即可．

解答 解：对于集合A，由x2-x-6≤0得，
所以，（x+2）（x-3）≤0，
解得，x∈[-2，3]，
即A={x|-2≤x≤3}，而B={x|x＞1}，
所以，A∩B={x|1＜x≤3}，
故答案为：B．

点评 本题主要考查了交集及其运算，涉及一元二次不等式的解法和集合的表示，属于基础题．

练习册系列答案
相关题目
15．化简：$\frac{cos（α+2π）•tan（α+π）}{sin（α-2π）}$得（　　）
A．1B．-1C．sin2αD．cos2α
16．已知f（x+1）定义域是[2，3]，求f（x2+2）定义域．
13．已知向量$\overrightarrow{a}$=（-2，5），|$\overrightarrow{b}$|=2|$\overrightarrow{a}$|，若$\overrightarrow{b}$与$\overrightarrow{a}$共线且反向，则$\overrightarrow{b}$=（4，-10）．
3．汽车的最佳使用年限是使年均消耗费用最低的年限（年均消耗费用=年均成本费+年均维修费），设某种汽车的购车的总费用为50000元；使用中每年的保险费、养路费及汽油费合计为6000元；前x年的总维修费y满足y=ax2+bx，已知第一年的维修费为1000元，前二年总维修费为3000元，这这种汽车的最佳使用年限为（　　）
A．8B．9C．10D．12
13．已知函数f（x）=$\frac{1}{2}{x^2}$+|x+1-2a|，其中a是实数．
（Ⅰ）判断f（x）的奇偶性，并说明理由；
（Ⅱ）当x∈[-1，1]时，f（x）的最小值为$\frac{1}{2}{a^2}$，求a的值．
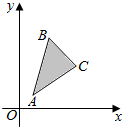20．给出平面区域如图所示，其中A（1，1），B（2，5），C（4，3）若使目标函数z=ax-y仅在点C处取得最大值，则a的取值范围是$（{\frac{2}{3}，+∞}）$．
17．等差数列{an}中，a2=3，a3+a4=9，则a1a6=14．
18．某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50]，[50，60]，…，[80，90]，[90，100]
（Ⅰ）求频率分布图中a的值；
（Ⅱ）估计该企业的职工对该部门评分不低于80的概率；
（Ⅲ）求出本次评分的众数、中位数、平均数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网