题目内容
已知x满足2log0.5x+1≤0,log0.5x+3≥0,求函数f(x)=(log2
)(log2
)的最值.
| x |
| 2 |
| x |
| 4 |
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:由条件求得 2≤x≤8,可得log2
和log2
的范围,从而求得函数f(x)=(log2
)(log2
)的最值.
| x |
| 2 |
| x |
| 4 |
| x |
| 2 |
| x |
| 4 |
解答:
解:由2log0.5x+1≤0,log0.5x+3≥0,可得-3≤log0.5x≤-1,∴2≤x≤8.
∴0≤log2
≤2,-1≤log2
≤1,∴-2≤(log2
)(log2
)≤2,
故f(x)=(log2
)(log2
)的最大值为2,最小值为-2.
∴0≤log2
| x |
| 2 |
| x |
| 4 |
| x |
| 2 |
| x |
| 4 |
故f(x)=(log2
| x |
| 2 |
| x |
| 4 |
点评:本题主要考查对数函数的值域,求二次函数在闭区间上的最值,二次函数的性质的应用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
若抛物线y2=2px(p>0)上横坐标是2的点M到抛物线焦点距离是3,则p=( )
| A、1 | B、2 | C、4 | D、8 |
 已知函数f(x)=Asin(ωt+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωt+φ)(A>0,ω>0,|φ|<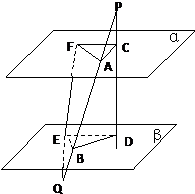 如图,线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,△ACF的面积为72,求△BDE的面积.
如图,线段PQ分别交两个平行平面α、β于A、B两点,线段PD分别交α、β于C、D两点,线段QF分别交α、β于F、E两点,若PA=9,AB=12,BQ=12,△ACF的面积为72,求△BDE的面积.